Vermoeiing
Verklarende woordenlijst
- Alternerende spanning
-
De alternerende spanning Sa is de mate waarin de spanning afwijkt van de gemiddelde spanning. Het wordt ook wel de spanningsamplitude genoemd.
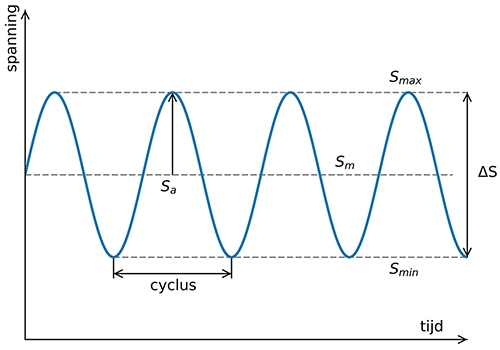
Fig. 1 Spanningsdefinities: Sa, Smin, Smax, Sm en ΔS
- Belastingsfactor
-
Historisch wordt de vermoeiingslimiet van materialen bepaald door middel van eenvoudige buigtesten, waardoor een spanningsgradiënt aanwezig is in het proefstuk. Een proefstuk belast in trek zal echter een lagere vermoeiingslimiet vertonen dan wanneer belast in buiging. De belastingsfactor is een empirische correctiefactor die met dit effect rekening houdt.
- Cyclische spanning-rek kromme
-
De vervorming van een materiaal tijdens een vermoeiingstest wordt gemeten in de vorm van een hysteresis-lus. Na enig initieel overgangsgedrag stabiliseert het materiaal en wordt dezelfde hysteresis-lus verkregen voor elke belastingscyclus. Elke geteste vervormingsreeks heeft een overeenkomstig spanningsinterval dat wordt gemeten. De cyclische spanning-vervormingcurve is een grafiek van al deze gegevens gecombineerd.
De curve beschrijft het gedrag van het materiaal nadat het plastisch is vervormd. Dit gedrag is meestal anders dan het initiële gedrag dat wordt gemeten bij een traditionele trekproef. Een eenvoudige machtsfunctie wordt ingepast aan deze curve om drie materiaaleigenschappen te verkrijgen: de cyclische sterktecoëfficiënt K', de cyclische vervormingshardheidsindex n' en de elasticiteitsmodulus E.
- Dang Van criterium
-
Het Dang Van criterium is een multiaxiaal vermoeiingslimiet criterium dat gebruikt wordt om de endurance limiet te voorspellen bij complexe belastingsgevallen. De uitkomst van de analyse wordt uitgedrukt als een veiligheidsfactor en dus niet als een levensduur. De methode gebruikt specifieke materiaalparameters bekomen uit trek- en torsieproeven.
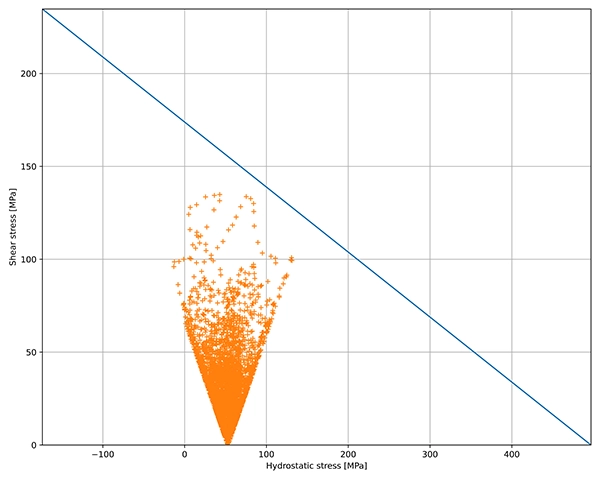
Fig. 2 De grafiek toont de Dang Van scatter plot (oranje stippen) in het kritische element van een onderdeel. Deze grafiek toont waar het belastingsverloop zich bevindt, in termen van microscopische schuifspanning en hydrostatische druk, ten opzichte van de drempelwaarde van het vermoeiingscriterium (blauwe lijn). Het komt er dus op neer dat vermoeiingsbreuk verwacht wordt wanneer de oranje stippen de blauwe lijn overschrijden.
- Gemiddelde spanning
-
De gemiddelde spanning Sm is het rekenkundig gemiddelde van de spanningen.
Zie Fig. 1 Spanningsdefinities
- Goodman diagram
-
Een positieve gemiddelde spanning (m.a.w. overwegend trekspanningen) verlaagt de vermoeiingslevensduur t.o.v. een gemiddelde spanning die gelijk is aan nul (m.a.w. een volledig terugkerende spanning tussen +S en -S). Het Goodman diagram, voor het eerst voorgesteld in 1890, is een grafische voorstelling van dit effect.
De alternerende spanning wordt geplot op de ene as en de gemiddelde spanning op de andere as. De toelaatbare alternerende spanning met een gemiddelde spanning gelijk aan nul, is de vermoeiingsgrens. De maximaal toelaatbare gemiddelde spanning is de uiterste trekspanning (m.a.w. niet-alternerend). Een rechte lijn wordt dan tussen die twee punten getrokken. Elke combinatie van de gemiddelde en de alternerende spanning op deze lijn zal dezelfde vermoeiingslevensduur tot gevolg hebben. Mathematisch wordt dit als volgt uitgedrukt:
$$\frac{S_a}{S_f} + \frac {S_m}{S_u} = 1$$
Sa is de alternerende spanning, Sm de gemiddelde spanning, Sf de volledig omkeerbare spanning (met Sm = 0) en Su de uiterste treksterkte van het materiaal.
- Groottefactor
-
Experimenten tonen aan dat grotere onderdelen een lagere vermoeiingslevensduur vertonen dan kleinere onderdelen. Aangezien de materiaaleigenschappen worden bekomen uit testen op kleine proefstukken, wordt een correctiefactor, de groottefactor genaamd, gebruikt voor grotere diameters. Voor niet-cirkelvormige doorsneden wordt een effectieve diameter berekend. De effectieve diameter wordt verkregen door het volume van het materiaal dat wordt blootgesteld aan 95% van de maximale spanning gelijk te stellen aan een ronde staaf in buiging met hetzelfde sterk belaste volume.
- Hysteresislus
-
De spanning-rek respons van een materiaal dat een alternerende belasting ondergaat, is in de vorm van een hysteresislus.
De hysteresislus wordt vaak gekarakteriseerd door de het spanningsinterval Δσ en het rekbereik Δε. Het rekbereik wordt vaak uitgesplitst in het elastische deel en het plastische deel van de totale rek.
- Maatfactor
-
Zie groottefactor
- Neuber's regel
-
Neuber's regel wordt gebruikt om een elastisch berekende spanning of rek om te zetten in de werkelijke spanning of rek wanneer plastische vervorming optreedt. Bijvoorbeeld, we kunnen een spanning berekenen in een kerf met elastische aannames als Kt·S en waarbij deze spanning de vloeisterkte van het materiaal overschrijdt. De werkelijke spanning zal ergens op de spannings-rekcurve van het materiaal liggen op een bepaald punt (ε-σ).
Neuber's regel stelt dat het product van de elastische spanning en rek, bekomen uit een elastische oplossing, gelijk is aan het product van de werkelijke elastisch-plastische oplossing. Wiskundig wordt dit uitgedrukt als:
$${\displaystyle {K _{t}}{S}\cdot{K _{t}}{e}={\sigma}\cdot{\varepsilon}}$$
- Nominale rek
-
De nominale rek is de rek voldoende ver weg van een lokale spanningsconcentratie.
- Nominale spanning
-
De nominale spanning is de spanning voldoende ver weg van een lokale spanningsconcentratie.
- Oneindige levensduur (infinite life)
-
Deze ontwerpfilosofie tegen vermoeiing streeft ernaar dat het onderdeel of de structuur een oneindig aantal belastingscycli kan doorstaan zonder falen, op voorwaarde dat de belastingen een bepaalde drempel niet overschrijden, zijnde de uithoudings- of vermoeiingsgrens. Als de toegepaste spanningen onder dit niveau blijven, zou het onderdeel theoretisch nooit mogen falen als gevolg van vermoeiing. Deze aanpak wordt vaak gebruikt bij kritieke onderdelen waar falen geen optie is, maar het kan leiden tot overmatig gewicht van het onderdeel en dus sterk verhoogde kosten.
Zie ook veilige levensduur, veilig falen en schadetolerantie.
- Oppervlakteafwerkingsfactor
-
De vermoeiingssterkte van een materiaal wordt bepaald via testen op kleine spiegel-gepolijste laboratoriummonsters. Een correctie op de oppervlakteafwerkingskwaliteit wordt toegepast op de vermoeiingssterkte van het materiaal om een inschatting te bekomen van de vermoeiingssterkte van een onderdeel in de toestand waarin het daadwerkelijk wordt gebruikt, namelijk bij de werkelijk oppervlaktekwaliteit van dat onderdeel.
Lees meer over de oppervlakteruwheidsfactor.
- Redundantie
-
Redundantie bij structuren verwijst naar het opzettelijk incorporeren van extra componenten, subsystemen of mechanismen in het ontwerp, die niet strikt noodzakelijk zijn voor de basisfunctionaliteit van de structuur, maar die dienen als back-up of alternatieve middelen om het falen van primaire componenten op te vangen. Deze extra elementen zorgen ervoor dat zelfs als één component faalt, de structuur nog steeds kan functioneren zoals bedoeld, zij het mogelijk met verminderde efficiëntie of capaciteit. Dit verhoogt over het algemeen de betrouwbaarheid en veiligheid van de structuur, omdat het de kans op totaal falen verkleint. Redundantie kan verschillende vormen aannemen, waaronder het dupliceren van cruciale componenten, het toevoegen van alternatieve belastingspaden, het implementeren van failsafe-mechanismen en het gebruik van overgedimensioneerde onderdelen.
- Rek-levensduur materiaalcurve
-
De rek-levensduurcurve wordt bepaald door het testen van materialen bij gecontroleerde rek. Het rekinterval wordt gecontroleerd en het overeenkomstige spanningsinterval en de vermoeiingslevensduur worden bepaald. Het is handig om de elastische en plastische spanningsamplitudes afzonderlijk te overwegen bij het inpassen van de testgegevens aan de materiaalcurve. Twee datapunten worden geplot voor elke test, één voor de elastische spanningsamplitude versus levensduur en een andere voor de plastische spanningsamplitude versus levensduur.
Vervolgens worden de testgegevens aangepast aan een eenvoudige machtsfunctie om de materiaalconstanten te verkrijgen: de vermoeiingsrekbaarheidscoëfficiënt εf', de vermoeiingsrekbaarheidsexponent c, de vermoeiingssterktecoëfficiënt σf' en de vermoeiingssterkte-exponent b.
De totale vervorming wordt vervolgens bekomen door de elastische en plastische componenten van de vervorming bij elkaar op te tellen.
- Schadetolerantie (damage tolerance)
-
Deze ontwerpfilosofie tegen vermoeiing erkent dat schade (zoals scheuren) zal optreden gedurende de levensduur van het onderdeel of de structuur. Het ontwerp moet de aanwezigheid van schade tolereren zonder dat dit leidt tot catastrofaal falen, zodat een veilige werking kan worden voortgezet totdat de schade kan worden gedetecteerd en gerepareerd. Dit houdt in dat een scheurgroei in de loop van de tijd wordt geëvalueerd, gebruikmakend van niet-destructieve testmethodes (NDT) om scheurtjes te monitoren, en inspectie-intervallen vast te stellen op basis van hoe snel scheurtjes kunnen groeien tot een kritieke grootte. Het is een proactieve benadering die tot doel heeft de veiligheid en integriteit te handhaven, zelfs in aanwezigheid van onverwachte vermoeiingsscheuren.
Zie ook oneindige levensduur, veilige levensduur en veilig falen.
- Spanning-levensduur kromme
-
De spanning-levensduur kromme is een grafische voorstelling van vermoeiingsdata. De kromme toont het verband tussen de vermoeiingslevensduur (in aantal cycli) en de spanningsamplitude of het spanningsinterval.
De meetdata wordt vaak gefit op een eenvoudige machtsfunctie die het verband tussen de spanningsamplitude (of het spanningsinterval) en de levensduur weergeeft. Het snijpunt met de y-as (de spanning) bij 1 cyclus wordt aangeduid met Sf' en de helling van de kromme met b. Wanneer testdata niet beschikbaar is, kan een benadering gebruikt worden op basis van de uiterste sterkte Su van het materiaal.
$${\displaystyle {S _{f}}^{\prime} = 1.6 \cdot {S _{u}} \ \ \text{en} \ \ {b = -0.085}}$$
- Spanningsamplitude
-
De spanningsamplitude Sa is de hoeveelheid spanning bovenop de gemiddelde spanning. De spanningsamplitude wordt ook wel de alternerende spanning genoemd.
Zie Fig. 1 Spanningsdefinities
- Spanningsconcentratiefactor
-
Spanningsconcentraties ontstaan bij een abrupte verandering in de geometrie van een belast onderdeel. Dit leidt tot een niet-uniforme spanningsverdeling over de dwarsdoorsnede van het onderdeel.
Een voorbeeld hiervan is een gat dat in een plaat is geboord. Wanneer een belasting P wordt opgelegd, verstoort de aanwezigheid van het gat de uniforme nominale spanning in de plaat. Het profiel van de normaalspanning in de dwarsdoorsnede door het midden van het gat heeft de vorm zoals te zien in onderstaande figuur (blauwe kleur). Merk op dat de maximale spanning σmax gelijk is aan Kt · σnom en optreedt aan de rand van het gat. De factor Kt staat bekend als de spanningsconcentratiefactor.
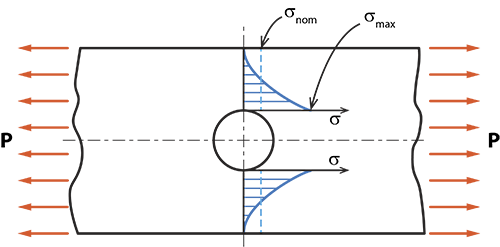
Fig. 3 Spanningsconcentratie nabij een gat in een plaat
- Spanningsinterval
-
Het spanningsinterval ΔS is de piek-tot-piek spanning.
Zie Fig. 1 Spanningsdefinities
- Uiterste sterkte
-
De uiterste sterkte Su wordt ook de treksterkte genoemd. Het is de maximale spanning die te zien is in een engineering spanning-rek diagram.
- Veilig falen (fail-safe)
-
Deze ontwerpfilosofie tegen vermoeiing is gebaseerd op de veronderstelling dat een bepaald niveau van vermoeiingsschade onvermijdelijk is. De focus ligt op het waarborgen dat een dergelijk falen niet leidt tot catastrofale gevolgen. Dit wordt bereikt door redundantie op te nemen, componenten zo te ontwerpen dat ze op een niet-catastrofale manier falen, of alternatieve belastingspaden te bieden zodat als één component faalt, de algehele structuur nog steeds veilig de belastingen kan dragen. Deze filosofie is gebruikelijk in systemen waar het falen van één component tot aanzienlijk gevaar kan leiden, zoals bij vliegtuigstructuren.
Zie ook oneindige levensduur, veilige levensduur en schadetolerantie.
- Veilige levensduur (safe-life)
-
Deze ontwerpfilosofie tegen vermoeiing hanteert een meer pragmatische benadering door een onderdeel zo te ontwerpen dat het een gegeven aantal belastingscycli met een hoge waarschijnlijkheid kan doorstaan. Deze ontwerpbenadering houdt rekening met de verwachte levensduur van het onderdeel, rekening houdend met de materiaaleigenschappen, verwachte belastingen en omgevingscondities. Na deze "veilige levensduur" heeft het onderdeel zijn bruikbare levensduur bereikt en moet het worden vervangen. Deze aanpak garandeert veiligheid en betrouwbaarheid tot een bepaald punt, maar houdt geen rekening met onverwachte overbelastingen of onopgemerkte scheurvorming.
Zie ook oneindige levensduur, veilig falen en schadetolerantie.
- Veiligheidsfactor
-
De veiligheidsfactor is hoeveel je de maximale sterkte van materialen wilt onderschatten om een veilig ontwerp te garanderen. Een enkele veiligheidsfactor wordt toegepast op zowel de spanningsamplitude als de gemiddelde spanning.
Dit kan grafisch worden weergegeven in het Goodman Diagram.
- Vermoeiingsgrens
-
Stalen proefstukken die in het laboratorium worden getest, vertonen een veilige spanning waarbij geen materiaalbezwijking zal optreden. Deze veilige spanning wordt de uithoudingsgrens of de vermoeiingsgrens genoemd. Dit gedrag wordt alleen gevonden bij staal. Bij aluminiumlegeringen wordt meestal de vermoeiingssterkte bij 107 cycli gebruikt in plaats van de vermoeiingsgrens. Dit is de spanning die materiaalfalen zal veroorzaken in 107 cycli.
- Vermoeiingskerffactor
-
Experimenten hebben aangetoond dat het effect van kleine kerven kleiner is dan het effect dat geschat wordt vanuit de traditionele spanningsconcentratiefactor Kt. De vermoeiingskerffactor Kf kan worden beschouwd als de effectieve spanningsconcentratie bij vermoeiing. Deze hangt af van de grootte van de spanningsconcentratie en van het materiaal. Kleine spanningsconcentraties zijn effectiever bij materialen met een hoge sterkte. Dit effect wordt verrekend aan de hand van een kerfgevoeligheidsfactor q:
$${\displaystyle {K _{f}} = 1 + ({{K _{t}} - 1})\cdot{q}}$$
De kerfgevoeligheidsfactor q is een empirisch bepaalde constante die afhankelijk is van de radius van de kerf en de materiaalsterkte.
- Vermoeiingslimiet
-
Zie vermoeiingsgrens
- Vermoeiingssterkte
-
De spanning die nodig is om fouten te veroorzaken in een gespecificeerd aantal cycli. Bij staal is dit meestal 106 cycli en voor lassen en aluminiumlegeringen is dit 107 cycli. De vermoeiingssterkte is direct gerelateerd aan de sterkte van het materiaal.
Een bruikbare benadering voor de vermoeiingssterkte is de helft van de uiteindelijke sterkte.
- Vervormingsamplitude
-
De vervormingsamplitude is de helft van het vervormingsinterval.
$$\varepsilon_a = \frac{\Delta \varepsilon}{2}$$
- Vervormingsinterval
-
Het vervormingsinterval Δε is de maximum vervorming min de minimum vervorming in een belasingscyclus:
$$\Delta \varepsilon = \varepsilon_{max} - \varepsilon_{min}$$
Onze opleidingen
Indien u meer wenst te leren over de Eindige Elementen Methode, kijk dan ook even naar onze opleiding Praktische Inleiding tot de Eindige Elementen Methode of onze opleiding Inleiding to vermoeiingsberekeningen met FEA.