Vermoeiingstesten van specimens worden gewoonlijk uitgevoerd op componenten met een spiegelgepolijst oppervlak. Onderdelen met een ruwere oppervlakteafwerking vertonen echter een verminderde vermoeiingssterkte. Om het effect van de opervlakteruwheid op de vermoeiingssterkte in rekening te brengen, wordt gebruik gemaakt van een oppervlakteruwheidsfactor KR. Deze oppervlakteruwheidsfactor wordt gebruikt om de materiaal S-N curve aan te passen. Dit artikel beschrijft de FKM methode voor het bepalen van de oppervlakteruwheidsfactor en hoe die toe te passen op de S-N curve.
FKM oppervlakteruwheidsfactor
De FKM-richtlijn Analytical Strength Assessment definieert de oppervlakteruwheidsfactor $K_R$ als volgt:
$${\displaystyle K_R=1-a_R \cdot log_{10}(R_Z) \cdot log_{10}\left(\frac {2R_m}{R_{m,N,min}}\right)}$$
Met:
- $R_Z$ de oppervlakteruwheid in µm volgens DIN 4768 (zie Tabel 2)
- $R_m$ de treksterkte in MPa
- $a_R$ een constante (zie Tabel 1)
- $R_{m,N,min}$ de minimum treksterkte in MPa (zie Tabel 1)
De ruwheidsfactor $K_R = 1$ voor een gepolijst oppervlak. Oppervlakteruwheden groter dan deze van een gepolijst oppervlak hebben waardes $K_R \lt 1$.
Tabel 1 hieronder geeft de waardes weer voor $R_{m,N,min}$ en voor de constante $a_R$ voor verschillende materiaal types.
| Materiaal type | aR | Rm,N,min [MPa] |
|---|---|---|
| Staal | 0.22 | 400 |
| GS | 0.20 | 400 |
| GGG | 0.16 | 400 |
| GT | 0.12 | 350 |
| GG | 0.06 | 100 |
| Aluminium smeedlegeringen | 0.22 | 133 |
| Aluminium gietlegeringen | 0.20 | 133 |
Tabel 2 hieronder voorziet een aantal indicatieve waardes voor de oppervlakteruwheid RZ van verschillende oppervlakteafwerkingen.
| Oppervlakteafwerking | Rz [µm] |
|---|---|
| Gepolijst | 0 |
| Geslepen | 12.5 |
| Machineafwerking | 100 |
| Ruwe machineafwerking | 200 |
| Gerold | 200 |
| Gegoten | 200 |
Voorbeeld berekening
Laten we als voorbeeld een staal met een treksterkte ${R_m = 600 \text{ MPa}}$ en met een gefreesde oppervlakteafwerking beschouwen.
In Tabel 1 vinden we voor staal: $a_R = 0.22$ en $R_{m,N,min} = 400 \text{ MPa}$. Tabel 2 geeft ons $R_Z = {100} \ {\mu m}$ voor machineafwerking.
Wanneer we deze waardes invoeren in de vergelijking van hierboven, dan krijgen we:
$${\displaystyle K_R=1-0.22 \cdot log_{10}(100)\cdot log_{10}\left( \frac{2 \cdot 600}{400}\right)} = 0.79$$
Constructie van de S-N curve
Voor we komen tot hoe de S-N curve aangepast wordt voor de berekende oppervlakteruwheidsfactor, laten we eerst eens kijken hoe de S-N curve is opgebouwd (zie Afbeelding 1 hieronder - klik voor een grotere afbeelding).
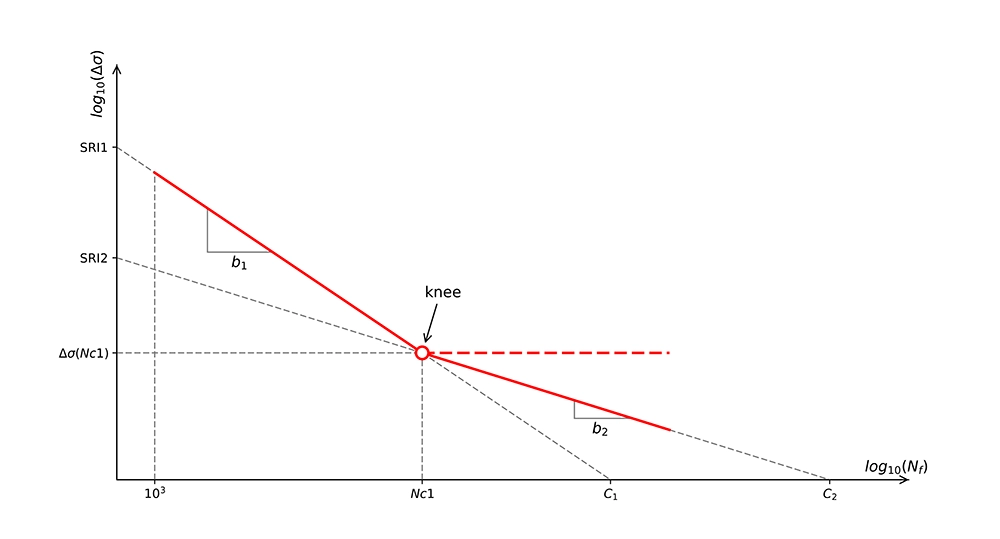
Voor het eerste deel van de S-N curve, met het aantal belastingcycli $N_f$ tussen 103 en $N_{c1}$ is de S-N curve gedefinieerd als:
$${\displaystyle \Delta \sigma(N_f) = SRI_1 \cdot N_f^{b_1}}$$
Het spanningsinterval $\Delta \sigma$ is een functie van het aantal cycli $N_f$. $SRI_1$ is het spanningsinterval snijpunt van de curve met de vertikale as bij één cyclus en $b_1$ is de helling van de curve, die een negatieve waarde is. De parameter $N_{c1}$ wordt het transitiepunt genoemd en is in wezen het aantal cycli waarbij een knik in de S-N curve waarneembaar is en de helling van de curve verandert. De waarde van $N_{c1}$ ligt gewoonlijk rond 106 - 107 cycli.
Voor $N_f \gt N_{c1}$ is de S-N curve gedefinieerd als:
$${\displaystyle \Delta \sigma(N_f) = SRI_2 \cdot N_f^{b_2}}$$
$SRI_2$ is het spanningsinterval snijpunt met de vertikale as bij één cyclus en $b_2$ is de helling van het tweede deel van de curve.
De parameters $SRI_1$, $N_{c1}$, $b_1$ en $b_2$ zijn materiaalparameters afgeleid van de vermoeiingstest data. SRI_2 kan als volgt afgeleid worden:
$${\displaystyle SRI_2 = SRI_1 \cdot (N_{c1})^{b_1-b_2}}$$
S-N curve aangepast voor de oppervlakteruwheidsfactor
De oppervlakteafwerking heeft de grootste invloed op het hoog-cyclische regime en wordt steeds kleiner richting de laag-cyclische regio. S-N curves worden gewoonlijk aangepast voor de oppervlakteruwheid door de helling $b_1$ in het eerste gedeelte van de S-N curve te wijzigen en de vermoeiingssterkte bij 1000 cycli gelijk te houden (zie Afbeelding 2 hieronder). De helling $b_2$ van het tweede deel van de S-N curve blijft ongewijzigd.
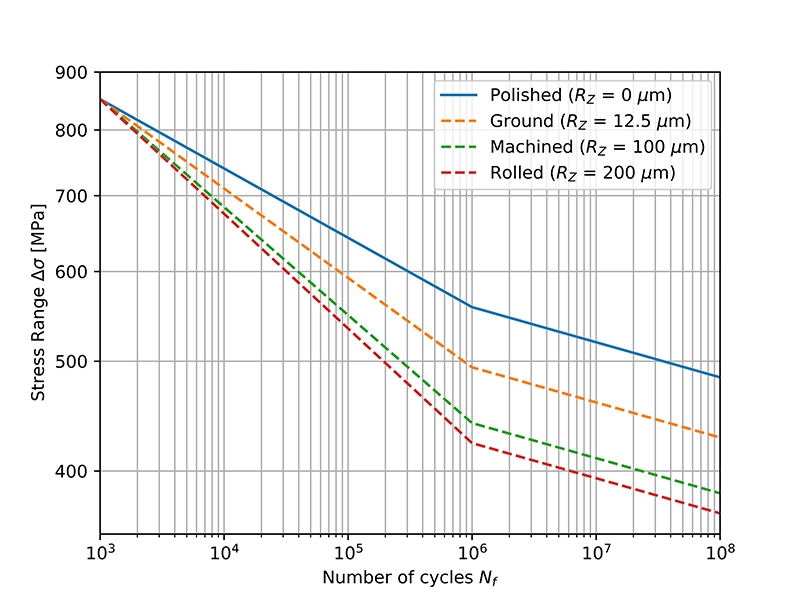
b1 = -0.0612 | b2 = -0.0310 | SRI1 = 1300 MPa | UTS = 600 MPa | Nc1 = 106 cycli
Laten we nu bekijken hoe de vergelijking van de S-N curve in Afbeelding 2 wordt aangepast voor de oppervlakteruwheidsfactor $K_R$. Voor de ongewijzigde curve (dus voor een gepolijst oppervlak), is het spanningsinterval bij $N_{c1}$ cycli:
$${\displaystyle \Delta \sigma(N_{c1}) = 1300 \cdot (10^6)^{-0.0612}=558.14 \text{ MPa}}$$
Het spanningsinterval $\Delta \sigma^{'}$ bij $N_{c1}$ cycli voor een gefreesd stalen onderdeel (met $K_R = 0.79$ berekend in het begin) wordt in ons geval:
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = K_R \cdot 558.14 = 440.97 \text{ MPa}}$$
$SRI_{1}^{'}$ en $b_{2}^{'}$ voor het eerste gedeelte van de aangepaste curve kan bepaald worden uit de volgende twee gelijkheden:
$${\displaystyle SRI_1 \cdot (10^3)^{b_1} = 851.81 = SRI_{1}^{'} \cdot (10^3)^{b^{'}_1}}$$
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = 440.97 = SRI_{1}^{'} \cdot (10^6)^{b_1^{'}}}$$
Wanneer we de vergelijkingen oplossen voor $SRI_{1}^{'}$ en $b_{1}^{'}$, vinden we:
$$SRI'_1 = 1645 \; \text{MPa en} \; b'_1 = -0.0953 $$
Aangezien $b_{2}^{'} = b_2$, kunnen we onderstaande vergelijking oplossen voor $SRI_{2}^{'}$:
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = 440.97 = SRI_{2}^{'} \cdot (10^6)^{b_2}}$$
Dit geeft ons $SRI_{2}^{'} = 677 \text{ MPa}$.
De vergelijking van de aangepaste S-N curve tussen 103 en $N_{c1}$ cycli wordt dan:
$${\displaystyle \Delta \sigma(N_{f}) = 1645 \cdot (N_f)^{-0.0953}}$$
En in de zone voor $N_f \gt N_{c1}$:
$${\displaystyle \Delta \sigma(N_{f}) = 677 \cdot (N_f)^{-0.0310}}$$