Les essais de fatigue des échantillons sont généralement réalisés sur des composants avec des surfaces polies miroir. Cependant, un composant avec une rugosité de surface plus élevée aura une résistance à la fatigue réduite. Pour tenir compte de l'effet de cette rugosité de surface sur la résistance à la fatigue d'un matériau, un facteur de rugosité KR est utilisé. Ce facteur de rugosité de surface est utilisé pour ajuster la courbe S-N du matériau. Cet article décrit la méthode FKM pour obtenir le facteur de rugosité de surface et comment appliquer ce facteur à la courbe S-N.
Facteur de rugosité de surface FKM
La directive FKM Évaluation analytique de la résistance définit le facteur de rugosité KR comme suit :
$${\displaystyle K_R=1-a_R \cdot log_{10}(R_Z) \cdot log_{10}\left(\frac {2R_m}{R_{m,N,min}}\right)}$$
Avec :
- RZ la rugosité de surface en µm selon DIN 4768 (voir Table 2)
- Rm la résistance à la traction en MPa
- aR une constante (voir Table 1)
- Rm,N,min la résistance à la traction minimale en MPa (voir Table 1)
Le facteur de rugosité KR = 1 pour une surface polie. Les rugosités de surface supérieures à celle d'une surface polie auront des valeurs de KR < 1.
La Table 1 ci-dessous donne les valeurs de Rm,N,min et de la constante aR pour différents types de matériaux.
| Type de matériau | aR | Rm,N,min [MPa] |
|---|---|---|
| Acier | 0.22 | 400 |
| GS | 0.20 | 400 |
| GGG | 0.16 | 400 |
| GT | 0.12 | 350 |
| GG | 0.06 | 100 |
| Alliages d'aluminium forgés | 0.22 | 133 |
| Alliages d'aluminium moulés | 0.20 | 133 |
La Table 2 ci-dessous fournit quelques valeurs indicatives pour la rugosité de surface RZ de différentes finitions de surface.
| État de surface | Rz [µm] |
|---|---|
| Poli | 0 |
| Rectifié | 12.5 |
| Usiné | 100 |
| Mal usiné | 200 |
| Laminé | 200 |
| Fondu | 200 |
Calcul d'exemple
À titre d'exemple, examinons un acier avec une résistance à la traction Rm = 600 MPa et avec une surface usinée.
Dans la Table 1, nous trouvons pour l'acier : aR = 0.22 et Rm,N,min = 400 MPa. La Table 2 nous donne RZ = 100 µm pour une surface usinée.
En insérant ces valeurs dans l'équation ci-dessus, nous obtenons :
$${\displaystyle K_R=1-0.22 \cdot log_{10}(100)\cdot log_{10}\left( \frac{2 \cdot 600}{400}\right)} = 0.79$$
Construction de la courbe S-N
Avant de voir comment la courbe S-N est ajustée pour le facteur de rugosité de surface, examinons comment la courbe S-N est construite (voir la Figure 1 ci-dessous - cliquez pour agrandir l'image).
Pour le nombre de cycles Nf entre 103 et Nc1 cycles, la courbe S-N est définie comme suit :
$${\displaystyle \Delta \sigma(N_f) = SRI_1 \cdot N_f^{b_1}}$$
L'amplitude de contrainte Δσ est une fonction du nombre de cycles Nf. SRI1 est l'interception de l'amplitude de contrainte à 1 cycle et b1 est la pente, qui est négative. Le paramètre Nc1 est appelé le Point de Transition de Fatigue et correspond essentiellement au nombre de cycles où une inflexion de la courbe de fatigue est perceptible. La valeur de Nc1 est généralement d'environ 106 - 107 cycles.
Pour Nf > Nc1, la courbe S-N est définie comme suit :
$${\displaystyle \Delta \sigma(N_f) = SRI_2 \cdot N_f^{b_2}}$$
SRI2 est l'interception de l'amplitude de contrainte à 1 cycle et b2 est la pente, qui est négative, pour la seconde partie de la courbe S-N.
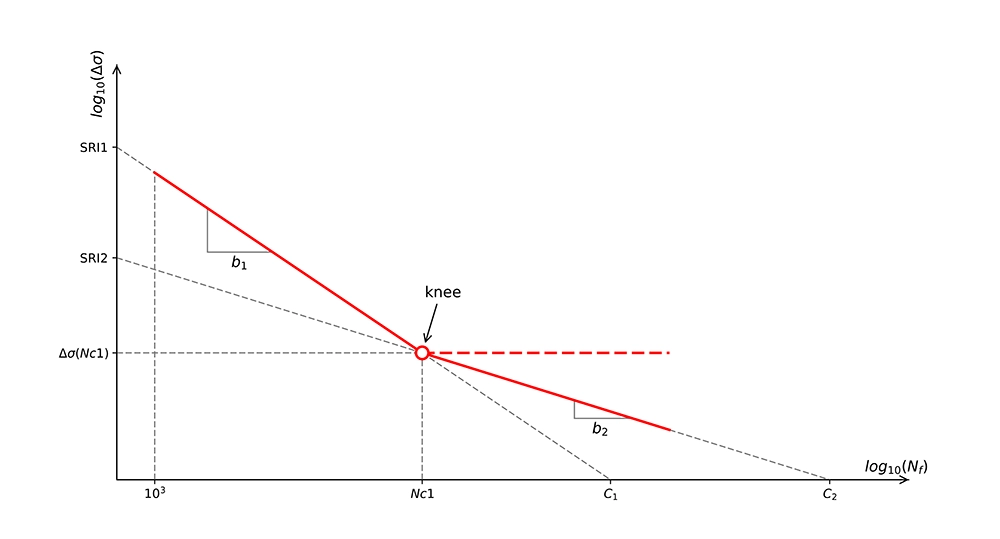
Les paramètres SRI1, Nc1, b1 et b2 sont des paramètres de matériau dérivés des données d'essai de fatigue. SRI2 peut être dérivé comme suit :
$${\displaystyle SRI_2 = SRI_1 \cdot (N_{c1})^{b_1-b_2}}$$
Courbe S-N ajustée pour le facteur de rugosité de surface
L'état de surface a le plus grand effet dans le régime mégacyclique et devient progressivement plus faible vers le régime oligocyclique. Les courbes S-N sont généralement ajustées pour la rugosité de surface en modifiant la pente b1 dans la première partie de la courbe S-N (voir la figure ci-dessous) tout en conservant la résistance à la fatigue à 1000 cycles identique. La pente b2 de la seconde partie de la courbe S-N reste inchangée.
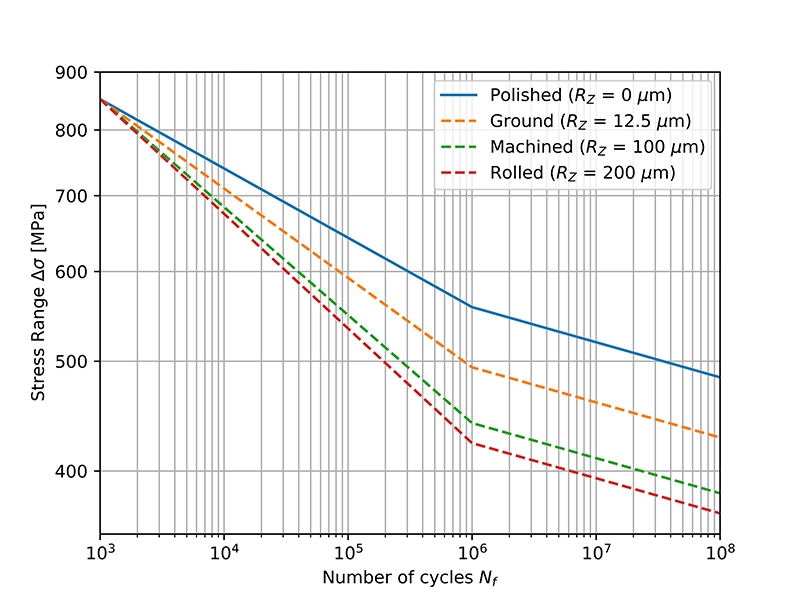
b1 = -0.0612 | b2 = -0.0310 | SRI1 = 1300 MPa | UTS = 600 MPa | Nc1 = 106 cycles
Voyons donc comment l'équation de la courbe S-N de la Figure 2 est modifiée. Pour la courbe non ajustée (surface polie), l'amplitude de contrainte à Nc1 cycles est :
$${\displaystyle \Delta \sigma(N_{c1}) = 1300 \cdot (10^6)^{-0.0612}=558.14 \text{ MPa}}$$
L'amplitude de contrainte Δσ' à Nc1 cycles pour une pièce usinée devient dans notre cas (avec KR = 0.79, comme calculé au début) :
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = K_R \cdot 558.14 = 440.97 \text{ MPa}}$$
SRI1' et b1' pour la première partie de la courbe modifiée peuvent être déterminés à partir des deux égalités ci-dessous :
$${\displaystyle SRI1 \cdot (10^3)^{b_1} = 851.81 = SRI_1^{'} \cdot (10^3)^{b^{'}_1}}$$
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = 440.97 = SRI_1^{'} \cdot (10^6)^{b_1^{'}}}$$
Lorsque nous résolvons pour SRI1' et b1', nous trouvons :
$$SRI'_1 = 1645 \; \text{MPa et} \; b'_1 = -0.0953 $$
Étant donné que b2' = b2, nous pouvons résoudre l'équation ci-dessous pour SRI2' :
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = 440.97 = SRI_2^{'} \cdot (10^6)^{b_2}}$$
Ce qui nous donne $SRI_{2}^{'} = 677 \text{ MPa}$
L'équation de la courbe S-N modifiée entre 103 et Nc1 cycles est alors :
$${\displaystyle \Delta \sigma(N_{f}) = 1645 \cdot (N_f)^{-0.0953}}$$
Et dans la région pour Nf > Nc1 :
$${\displaystyle \Delta \sigma(N_{f}) = 677 \cdot (N_f)^{-0.0310}}$$