Fatigue tests of specimens are usually done on components with mirror polished surfaces. However, a component with a larger surface roughness will have a reduced fatigue strength. To account for the effect of this surface roughness to the fatigue strength of a material, a roughness factor KR is used. This surface roughness factor is used to adjust the material S-N curve. This article describes the FKM method for obtaining the surface roughness factor and how to apply this factor to the S-N curve.
FKM surface roughness factor
The FKM-guideline Analytical Strength Assessment defines the roughness factor KR as follows:
$${\displaystyle K_R=1-a_R \cdot log_{10}(R_Z) \cdot log_{10}\left(\frac {2R_m}{R_{m,N,min}}\right)}$$
With:
- RZ the surface roughness in µm according to DIN 4768 (see Table 2)
- Rm the tensile strength in MPa
- aR a constant (see Table 1)
- Rm,N,min the minimum tensile strength in MPa (see Table 1)
The roughness factor KR = 1 for a polished surface. Surface roughnesses higher than that of a polished surface will have values for KR < 1.
Table 1 below gives the values for Rm,N,min and for constant aR for different material types.
| Material Type | aR | Rm,N,min [MPa] |
|---|---|---|
| Steel | 0.22 | 400 |
| GS | 0.20 | 400 |
| GGG | 0.16 | 400 |
| GT | 0.12 | 350 |
| GG | 0.06 | 100 |
| Wrought aluminium alloys | 0.22 | 133 |
| Cast aluminium alloys | 0.20 | 133 |
Table 2 below provides some indicative values for the surface roughness RZ of different surface finishes.
| Surface Condition | Rz [µm] |
|---|---|
| Polished | 0 |
| Ground | 12.5 |
| Machined | 100 |
| Poor machined | 200 |
| Rolled | 200 |
| Cast | 200 |
Example calculation
As an example, let's look at a steel with a tensile strength Rm = 600 MPa and with a machined surface.
In Table 1 we find for Steel: aR = 0.22 and Rm,N,min = 400 MPa. Table 2 gives us RZ = 100 µm for a machined surface.
Putting these values in the above equation gives us:
$${\displaystyle K_R=1-0.22 \cdot log_{10}(100)\cdot log_{10}\left( \frac{2 \cdot 600}{400}\right)} = 0.79$$
Construction of the S-N curve
Before we get to how the S-N curve is adjusted for the surface roughness factor, let's look at how the S-N curve is constructed (see Figure 1 below - click for larger image).
For the number of cycles Nf between 103 and Nc1 cycles, the S-N curve is defined as:
$${\displaystyle \Delta \sigma(N_f) = SRI_1 \cdot N_f^{b_1}}$$
The stress range Δσ is a function of the number of cycles Nf. SRI1 is the stress range intercept at 1 cycle and b1 is the slope, which is negative. The parameter Nc1 is called the Fatigue Transition Point and is basically the number of cycles by which a kink in the fatigue curve is noticeable. The value of Nc1 is usually around 106 - 107 cycles.
For Nf > Nc1, the S-N curve is defined as:
$${\displaystyle \Delta \sigma(N_f) = SRI_2 \cdot N_f^{b_2}}$$
SRI2 is the stress range intercept at 1 cycle and b2 is the slope, which is negative, for the second part of the S-N curve.
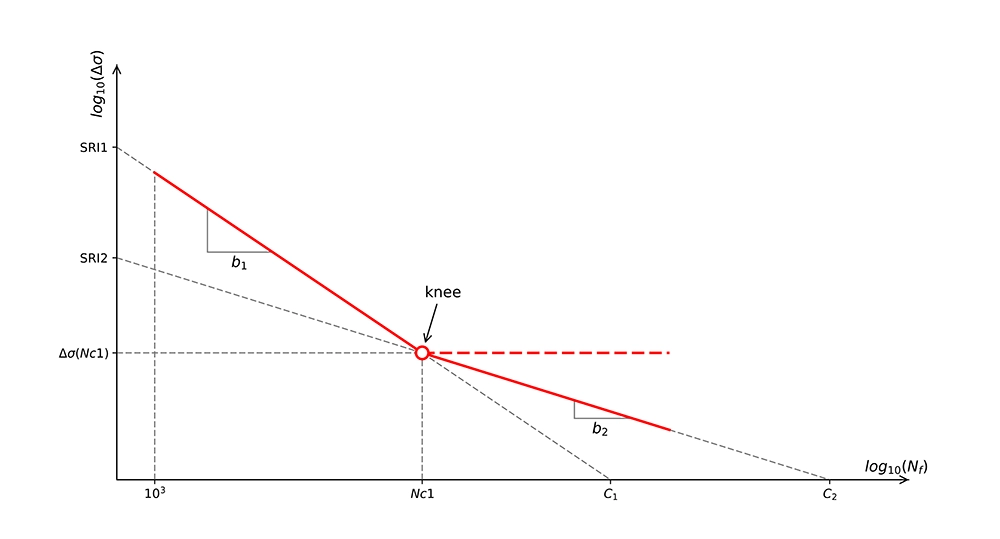
The parameters SRI1, Nc1, b1 and b2 are material parameters derived from the fatigue test data. SRI2 can be derived as follows:
$${\displaystyle SRI_2 = SRI_1 \cdot (N_{c1})^{b_1-b_2}}$$
S-N curve adjusted for the surface roughness factor
The surface condition has the greatest effect in the high-cycle regime and becomes progressively smaller towards the low-cycle regime. S-N curves are usually adjusted for the surface roughness by changing the slope b1 in the first part of the S-N curve (see figure below) and keeping the fatigue strength at 1000 cycles the same. The slope b2 of the second part of the S-N curve remains unchanged.
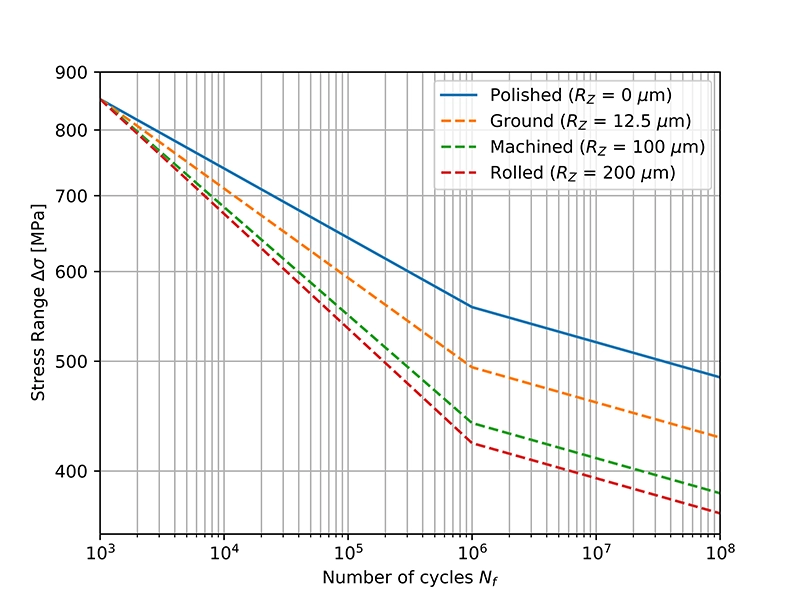
b1 = -0.0612 | b2 = -0.0310 | SRI1 = 1300 MPa | UTS = 600 MPa | Nc1 = 106 cycles
So, let's find out how the equation of the S-N curve in Figure 2 is modified. For the unadjusted curve (polished surface), the stress range at Nc1 cycles is:
$${\displaystyle \Delta \sigma(N_{c1}) = 1300 \cdot (10^6)^{-0.0612}=558.14 \text{ MPa}}$$
The stress range Δσ' at Nc1 cycles for a machined part becomes in our case (with KR = 0.79, as calculated in the beginning):
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = K_R \cdot 558.14 = 440.97 \text{ MPa}}$$
SRI1' and b1' for the first part of the modified curve can be determined from the two equalities below:
$${\displaystyle SRI1 \cdot (10^3)^{b_1} = 851.81 = SRI_1^{'} \cdot (10^3)^{b^{'}_1}}$$
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = 440.97 = SRI_1^{'} \cdot (10^6)^{b_1^{'}}}$$
When we solve for SRI1' and b1', we find:
$$SRI'_1 = 1645 \; \text{MPa and} \; b'_1 = -0.0953 $$
Since b2' = b2, we can solve below equation for SRI2':
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = 440.97 = SRI_2^{'} \cdot (10^6)^{b_2}}$$
Which gives us $SRI_{2}^{'} = 677 \text{ MPa}$
The equation of the modified S-N curve between 103 and Nc1 cycles is then:
$${\displaystyle \Delta \sigma(N_{f}) = 1645 \cdot (N_f)^{-0.0953}}$$
And in the region for Nf > Nc1:
$${\displaystyle \Delta \sigma(N_{f}) = 677 \cdot (N_f)^{-0.0310}}$$