Ermüdungstests an Proben werden normalerweise an Komponenten mit spiegelpolierten Oberflächen durchgeführt. Eine Komponente mit einer größeren Oberflächenrauheit weist jedoch eine reduzierte Ermüdungsfestigkeit auf. Um den Einfluss dieser Oberflächenrauheit auf die Ermüdungsfestigkeit eines Materials zu berücksichtigen, wird ein Rauheitsfaktor KR verwendet. Dieser Oberflächenrauheitsfaktor wird verwendet, um die Material-S-N-Kurve anzupassen. Dieser Artikel beschreibt die FKM-Methode zur Bestimmung des Oberflächenrauheitsfaktors und wie dieser Faktor auf die S-N-Kurve angewendet wird.
FKM-Oberflächenrauheitsfaktor
Die FKM-Richtlinie Analytische Festigkeitsbewertung definiert den Rauheitsfaktor KR wie folgt:
$${\displaystyle K_R=1-a_R \cdot log_{10}(R_Z) \cdot log_{10}\left(\frac {2R_m}{R_{m,N,min}}\right)}$$
Mit:
- RZ die Oberflächenrauheit in µm gemäß DIN 4768 (siehe Tabelle 2)
- Rm die Zugfestigkeit in MPa
- aR eine Konstante (siehe Tabelle 1)
- Rm,N,min die Mindestzugfestigkeit in MPa (siehe Tabelle 1)
Der Rauheitsfaktor KR = 1 für eine polierte Oberfläche. Oberflächenrauheiten, die größer sind als die einer polierten Oberfläche, haben Werte für KR < 1.
Die Tabelle 1 unten gibt die Werte für Rm,N,min und für die Konstante aR für verschiedene Materialtypen an.
| Materialtyp | aR | Rm,N,min [MPa] |
|---|---|---|
| Stahl | 0.22 | 400 |
| GS | 0.20 | 400 |
| GGG | 0.16 | 400 |
| GT | 0.12 | 350 |
| GG | 0.06 | 100 |
| Verformte Aluminiumlegierungen | 0.22 | 133 |
| Gegossene Aluminiumlegierungen | 0.20 | 133 |
Die Tabelle 2 unten gibt einige Richtwerte für die Oberflächenrauheit RZ verschiedener Oberflächenbearbeitungen an.
| Oberflächenzustand | Rz [µm] |
|---|---|
| Poliert | 0 |
| Geschliffen | 12,5 |
| Bearbeitet | 100 |
| Schlecht bearbeitet | 200 |
| Walzblank | 200 |
| Gegossen | 200 |
Beispielrechnung
Als Beispiel betrachten wir einen Stahl mit einer Zugfestigkeit Rm = 600 MPa und einer bearbeiteten Oberfläche.
In Tabelle 1 finden wir für Stahl: aR = 0,22 und Rm,N,min = 400 MPa. Tabelle 2 gibt uns RZ = 100 µm für eine bearbeitete Oberfläche.
Setzen wir diese Werte in die obige Gleichung ein, erhalten wir:
$${\displaystyle K_R=1-0.22 \cdot log_{10}(100)\cdot log_{10}\left( \frac{2 \cdot 600}{400}\right)} = 0.79$$
Aufbau der S-N-Kurve
Bevor wir darauf eingehen, wie die S-N-Kurve für den Oberflächenrauheitsfaktor angepasst wird, sehen wir uns an, wie die S-N-Kurve konstruiert wird (siehe Abbildung 1 unten - zum Vergrößern klicken).
Für die Anzahl der Zyklen Nf zwischen 103 und Nc1 Zyklen ist die S-N-Kurve definiert als:
$${\displaystyle \Delta \sigma(N_f) = SRI_1 \cdot N_f^{b_1}}$$
Die Spannungsamplitude Δσ ist eine Funktion der Anzahl der Zyklen Nf. SRI1 ist der Spannungsbereichsabgriff bei 1 Zyklus und b1 ist die Steigung, die negativ ist. Der Parameter Nc1 wird als Ermüdungsübergangspunkt bezeichnet und ist im Grunde die Anzahl der Zyklen, bei denen ein Knick in der Ermüdungskurve erkennbar ist. Der Wert von Nc1 liegt normalerweise bei etwa 106 - 107 Zyklen.
Für Nf > Nc1 ist die S-N-Kurve definiert als:
$${\displaystyle \Delta \sigma(N_f) = SRI_2 \cdot N_f^{b_2}}$$
SRI2 ist der Spannungsbereichsabgriff bei 1 Zyklus und b2 ist die Steigung, die negativ ist, für den zweiten Teil der S-N-Kurve.
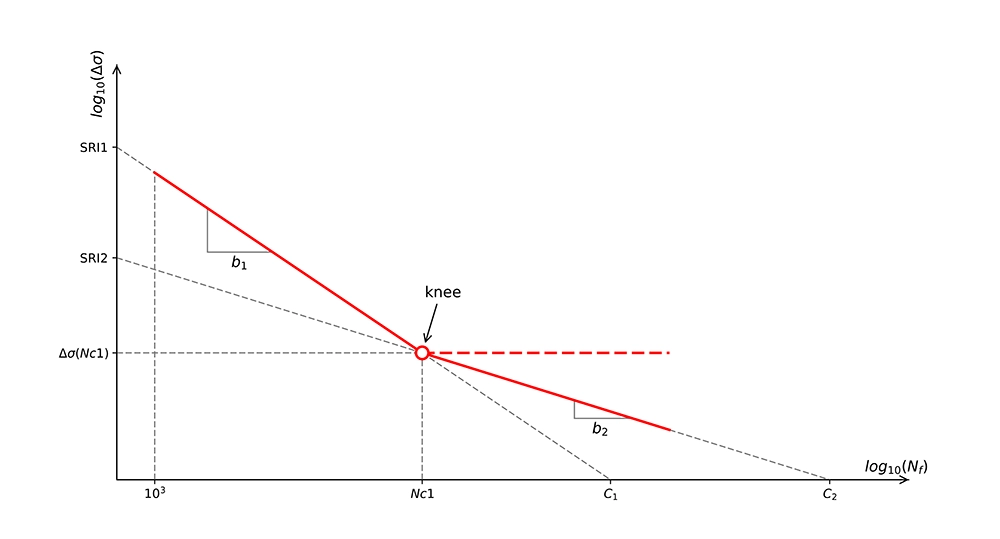
Die Parameter SRI1, Nc1, b1 und b2 sind Materialparameter, die aus den Ermüdungsprüfdaten abgeleitet werden. SRI2 kann wie folgt abgeleitet werden:
$${\displaystyle SRI_2 = SRI_1 \cdot (N_{c1})^{b_1-b_2}}$$
S-N-Kurve, angepasst für den Oberflächenrauheitsfaktor
Der Oberflächenzustand hat den größten Einfluss im Hochzyklusbereich und wird im Niedrigzyklusbereich immer kleiner. S-N-Kurven werden normalerweise für die Oberflächenrauheit angepasst, indem die Steigung b1 im ersten Teil der S-N-Kurve geändert wird (siehe Abbildung unten) und die Ermüdungsfestigkeit bei 1000 Zyklen gleich bleibt. Die Steigung b2 des zweiten Teils der S-N-Kurve bleibt unverändert.
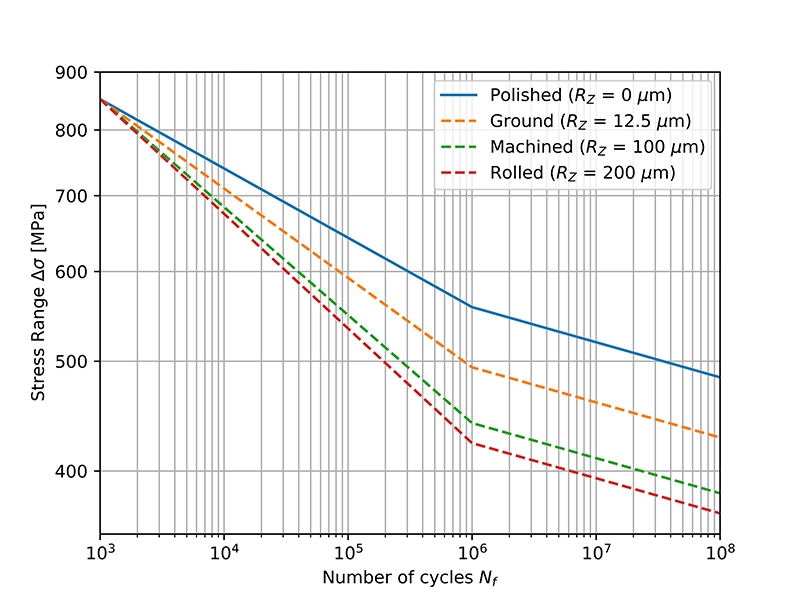
b1 = -0,0612 | b2 = -0,0310 | SRI1 = 1300 MPa | UTS = 600 MPa | Nc1 = 106 Zyklen
Ermitteln wir also, wie die Gleichung der S-N-Kurve in Abbildung 2 modifiziert wird. Für die unmodifizierte Kurve (polierte Oberfläche) ist der Spannungsbereich bei Nc1 Zyklen:
$${\displaystyle \Delta \sigma(N_{c1}) = 1300 \cdot (10^6)^{-0.0612}=558.14 \text{ MPa}}$$
Der Spannungsbereich Δσ' bei Nc1 Zyklen für ein bearbeitetes Teil wird in unserem Fall (mit KR = 0,79, wie zu Beginn berechnet):
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = K_R \cdot 558.14 = 440.97 \text{ MPa}}$$
SRI1' und b1' für den ersten Teil der modifizierten Kurve können aus den beiden Gleichungen unten bestimmt werden:
$${\displaystyle SRI1 \cdot (10^3)^{b_1} = 851.81 = SRI_1^{'} \cdot (10^3)^{b^{'}_1}}$$
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = 440.97 = SRI_1^{'} \cdot (10^6)^{b_1^{'}}}$$
Wenn wir nach SRI1' und b1' auflösen, erhalten wir:
$$SRI'_1 = 1645 \; \text{MPa und} \; b'_1 = -0.0953 $$
Da b2' = b2, können wir die folgende Gleichung nach SRI2' lösen:
$${\displaystyle \Delta \sigma^{'}(N_{c1}) = 440.97 = SRI_2^{'} \cdot (10^6)^{b_2}}$$
Was uns $SRI_{2}^{'} = 677 \text{ MPa}$ ergibt.
Die Gleichung der modifizierten S-N-Kurve zwischen 103 und Nc1 Zyklen lautet dann:
$${\displaystyle \Delta \sigma(N_{f}) = 1645 \cdot (N_f)^{-0.0953}}$$
Und im Bereich für Nf > Nc1:
$${\displaystyle \Delta \sigma(N_{f}) = 677 \cdot (N_f)^{-0.0310}}$$