Der Standardfehler SE von log10(N) wird verwendet, um die vorhergesagte Ermüdungslebensdauer oder den Schaden auf jede gewünschte Überlebenswahrscheinlichkeit anzupassen. Ermüdungslebensdauerdaten weisen immer eine gewisse Streuung auf, und bei jedem gegebenen Spannungsniveau wird angenommen, dass die Verteilung der Ermüdungslebensdauer einer log-normalen Verteilung folgt. Anders ausgedrückt, handelt es sich um eine Normal- oder Gaußverteilung des Logarithmus der Ermüdungslebensdauer.
Der Standardfehler
In der Praxis verwenden wir eine Lookup-Tabelle (siehe Tabelle 1 unten), um die Abweichung von der mittleren (50%) Lebensdauer in Bezug auf die Anzahl der Standardfehler zu bestimmen, wenn wir eine Lebens- oder Schadensvorhersage basierend auf einem bestimmten Prozentsatz der Überlebenswahrscheinlichkeit treffen möchten.
Die Werte in der Tabelle werden mithilfe der Dichtefunktion (PDF) und der Kumulativen Dichtefunktion (CDF) der Normalverteilung berechnet.
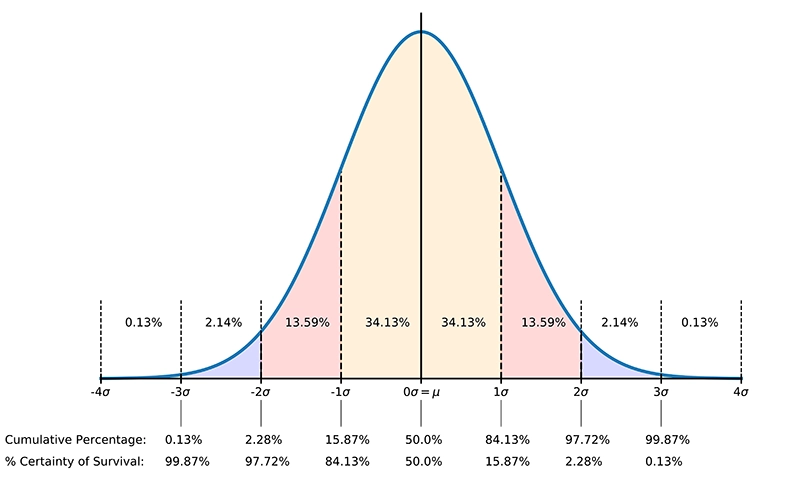
Die Dichtefunktion (PDF) ist die in Abbildung 1 unten gezeigte Normalverteilungskurve:
$${\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}\;\exp \left(-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right)}$$
Mit:
- $\mu$ dem Mittelwert der Daten
- $\sigma$ der Standardabweichung des Mittelwerts
Die Kumulative Dichtefunktion ist das Integral der PDF:
$${\displaystyle {\frac {1}{2}}\left(1+\mathrm {erf} \,{\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)}$$
Die prozentuale Überlebenswahrscheinlichkeit ist dann 1 - CDF (siehe auch Abbildung 1).
| Anzahl der SDs vom Mittelwert |
% Überlebenswahrscheinlichkeit |
|---|---|
| -5 | 99,99997 |
| -4 | 99,997 |
| -3 | 99,87 |
| -2 | 97,72 |
| -1 | 84,13 |
| 0 | 50 |
| 1 | 15,87 |
| 2 | 2,28 |
| 3 | 0,13 |
| 4 | 0,003 |
| 5 | 0,00003 |
Berechnungsbeispiel
Angenommen, wir haben ein Bauteil, das einer zyklischen Spannung mit konstanter Amplitude ausgesetzt ist, die zwischen ±300 MPa schwankt. Das Bauteil besteht aus einem Material, für das wir die Parameter der S-N-Kurve für eine Überlebenswahrscheinlichkeit von 50% kennen. Diese Parameter sind:
- Spannungsbereichsinterzept SRI = 1300 MPa
- die Steigung der Kurve b1 = -0,0612
- Standardfehler SE = 0,12
Die oben genannten Parameter definieren eine S-N-Kurve in Bezug auf den Spannungsbereich, nicht die Spannungsamplitude. Der Spannungsbereich Sr ist eine Funktion der Anzahl der Lastwechsel bis zum Versagen N:
$${\displaystyle S_r = SRI \cdot N^{b_1}}$$
In unserem Fall beträgt der Spannungsbereich 2 ⋅ 300 MPa = 600 MPa. Die vorhergesagte Anzahl der Lastwechsel bis zum Versagen des Bauteils, basierend auf einer Überlebenswahrscheinlichkeit von 50% S-N-Kurve, wird sein:
$${\displaystyle 600 = 1300 \cdot N_{50}^{-0.0612}}$$
oder N50 = 306760 Zyklen.
Wir möchten nun die Design-S-N-Kurve verwenden (typischerweise wird in den meisten Designs eine Überlebenswahrscheinlichkeit von 97,7% verwendet) und nicht die mittlere S-N-Kurve. Wie viele Lastwechsel bis zum Versagen werden für das Bauteil basierend auf der S-N-Kurve mit einer Überlebenswahrscheinlichkeit von 97,7% vorhergesagt?
Zuerst müssen wir die Anzahl der Standardabweichungen n vom Mittelwert herausfinden, die einer Überlebenswahrscheinlichkeit von 97,7% entspricht. In Tabelle 1 finden wir n = -2 für eine Überlebenswahrscheinlichkeit von 97,7%.
Die S-N-Kurve wird angepasst, indem die Kurve nach links verschoben wird, oder anders ausgedrückt, indem die Anzahl der Lastwechsel reduziert wird:
$${\displaystyle log_{10}(N) = log_{10}(N_{50}) - n \cdot SE}$$
oder anders ausgedrückt:
$${\displaystyle N = N_{50} \cdot 10^{(-n \text{ } \cdot \text{ } SE)}}$$
$${\displaystyle N_{97.7} = 306760 \cdot 10^{(-2 \text{ } \cdot \text{ } 0.12)}}$$
Das ergibt ${\displaystyle S_{97.7}}$ = 176522 Zyklen, also eine Reduzierung der Ermüdungslebensdauer um 42% im Vergleich zu N50.