L'erreur standard ES de log10(N) est utilisée pour ajuster la durée de vie en fatigue ou les dommages prédits à une probabilité donnée de survie. Les données sur la durée de vie en fatigue incluent toujours une certaine dispersion, et à un niveau de contrainte donné, la distribution des durées de vie en fatigue est supposée être une distribution log-normale. Autrement dit, une distribution normale ou de Gauss du logarithme de la durée de vie en fatigue.
L'erreur standard
En pratique, si l'on veut faire une prédiction de la durée de vie ou des dommages basée sur un pourcentage particulier de probabilité de survie, on utilise une table de consultation (voir Tableau 1 ci-dessous) pour déterminer l'écart par rapport à la durée de vie moyenne (50%) en termes de nombre d'erreurs standard.
Les valeurs du tableau sont calculées à l'aide de la Fonction de Densité de Probabilité (FDP) et de la Fonction de Répartition Cumulative (FRC) de la distribution normale.
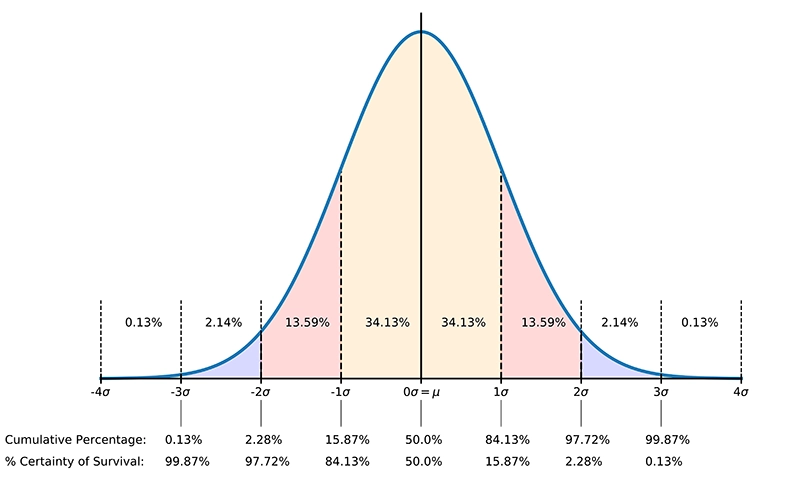
La Fonction de Densité de Probabilité (FDP) est la courbe de distribution normale illustrée à la Figure 1 ci-dessous :
$${\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}\;\exp \left(-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right)}$$
Avec :
- $\mu$ la moyenne des données
- $\sigma$ l'écart type de la moyenne
La Fonction de Répartition Cumulative est l'intégrale de la FDP :
$${\displaystyle {\frac {1}{2}}\left(1+\mathrm {erf} \,{\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)}$$
La certitude de survie en pourcentage est alors 1 - FRC (voir également Figure 1).
| Nombre d'ES par rapport à la moyenne |
% Certitude de Survie |
|---|---|
| -5 | 99,99997 |
| -4 | 99,997 |
| -3 | 99,87 |
| -2 | 97,72 |
| -1 | 84,13 |
| 0 | 50 |
| 1 | 15,87 |
| 2 | 2,28 |
| 3 | 0,13 |
| 4 | 0,003 |
| 5 | 0,00003 |
Exemple de calcul
Par exemple, disons que nous avons un composant soumis à une contrainte cyclique à amplitude constante, oscillant entre ±300 MPa. Le composant est fait d'un matériau pour lequel nous connaissons les paramètres de la courbe S-N pour une certitude de survie de 50%. Ces paramètres sont :
- interception de la plage de contrainte SRI = 1300 MPa
- pente de la courbe b1 = -0,0612
- erreur standard ES = 0,12
Les paramètres ci-dessus définissent une courbe S-N en termes de plage de contrainte, et non d'amplitude de contrainte. La plage de contrainte Sr est une fonction du nombre de cycles jusqu'à la rupture N :
$${\displaystyle S_r = SRI \cdot N^{b_1}}$$
Dans notre cas, la plage de contrainte est de 2 ⋅ 300 MPa = 600 MPa. Le nombre de cycles prédit jusqu'à la rupture du composant, basé sur une courbe S-N avec une certitude de survie de 50%, sera :
$${\displaystyle 600 = 1300 \cdot N_{50}^{-0.0612}}$$
ou N50 = 306760 cycles.
Nous voulons maintenant utiliser la courbe S-N de conception (généralement une certitude de survie de 97,7% est utilisée dans la plupart des conceptions) et non la courbe S-N moyenne. Quel est le nombre de cycles prédit auquel le composant échouera, basé sur une courbe S-N avec une certitude de survie de 97,7%?
D'abord, nous devons trouver le nombre d'écarts types n par rapport à la moyenne qui correspond à une certitude de survie de 97,7%. Dans le Tableau 1, nous trouvons n = -2 pour une certitude de survie de 97,7%.
La courbe S-N est ajustée en déplaçant la courbe vers la gauche, ou autrement dit, en réduisant le nombre de cycles :
$${\displaystyle log_{10}(N) = log_{10}(N_{50}) - n \cdot SE}$$
ou exprimé d'une autre manière :
$${\displaystyle N = N_{50} \cdot 10^{(-n \text{ } \cdot \text{ } SE)}}$$
$${\displaystyle N_{97.7} = 306760 \cdot 10^{(-2 \text{ } \cdot \text{ } 0.12)}}$$
Cela nous donne ${\displaystyle S_{97.7}}$ = 176522 cycles, soit une réduction de 42% de la durée de vie en fatigue par rapport à N50.