Die Ramberg-Osgood-Gleichung

Die Ramberg-Osgood-Beziehung

Das Hookesche Gesetz besagt, dass unterhalb der Fließgrenze die Spannung linear proportional zur Dehnung ist:

$${\sigma = {E} \; {\varepsilon}_{e}}$$

Ramberg und Osgood definierten ein Potenzgesetz zur Beschreibung der plastischen Dehnung:

$${{\varepsilon}_{p} = \left(\frac{\sigma}{K} \right)^n}$$

Die werkstoffabhängigen Parameter $K$ und $n$ beschreiben das Verfestigungsverhalten des Materials.

Die Gesamtdehnung ${\varepsilon}_{t}$ ist die Summe aus elastischer Dehnung ${\varepsilon}_{e}$ und plastischer Dehnung ${\varepsilon}_{p}$, woraus sich ergibt:

$${{\varepsilon}_{t} = {\varepsilon}_{e} + {\varepsilon}_{p} = \frac{\sigma}{E} + \left(\frac{\sigma}{K} \right)^n}$$

Mit:

• ${\varepsilon}$ die Dehnung
• ${\sigma}$ die Spannung
• $K$ nichtlinearer Werkstoffmodul
• $n$ Verfestigungsexponent des Werkstoffs

Genauigkeit der Gleichung

Die Gleichung ist keine perfekte Abbildung des tatsächlichen Spannungs-Dehnungs-Verhaltens des Werkstoffs, da die Ramberg-Osgood-Gleichung impliziert, dass plastische Dehnung bei jedem Spannungsniveau vorhanden ist, auch weit unterhalb der Fließgrenze. Allerdings ist der plastische Dehnungsanteil an der Gesamtdehnung bei niedrigen Spannungsniveaus sehr gering.

Manche Werkstoffe zeigen einen abrupten Steifigkeitswechsel beim Fließen. In diesem Fall bildet die Ramberg-Osgood-Beziehung den Bereich um die Fließgrenze nicht gut ab (siehe Abbildung 1 unten).

Beispiel

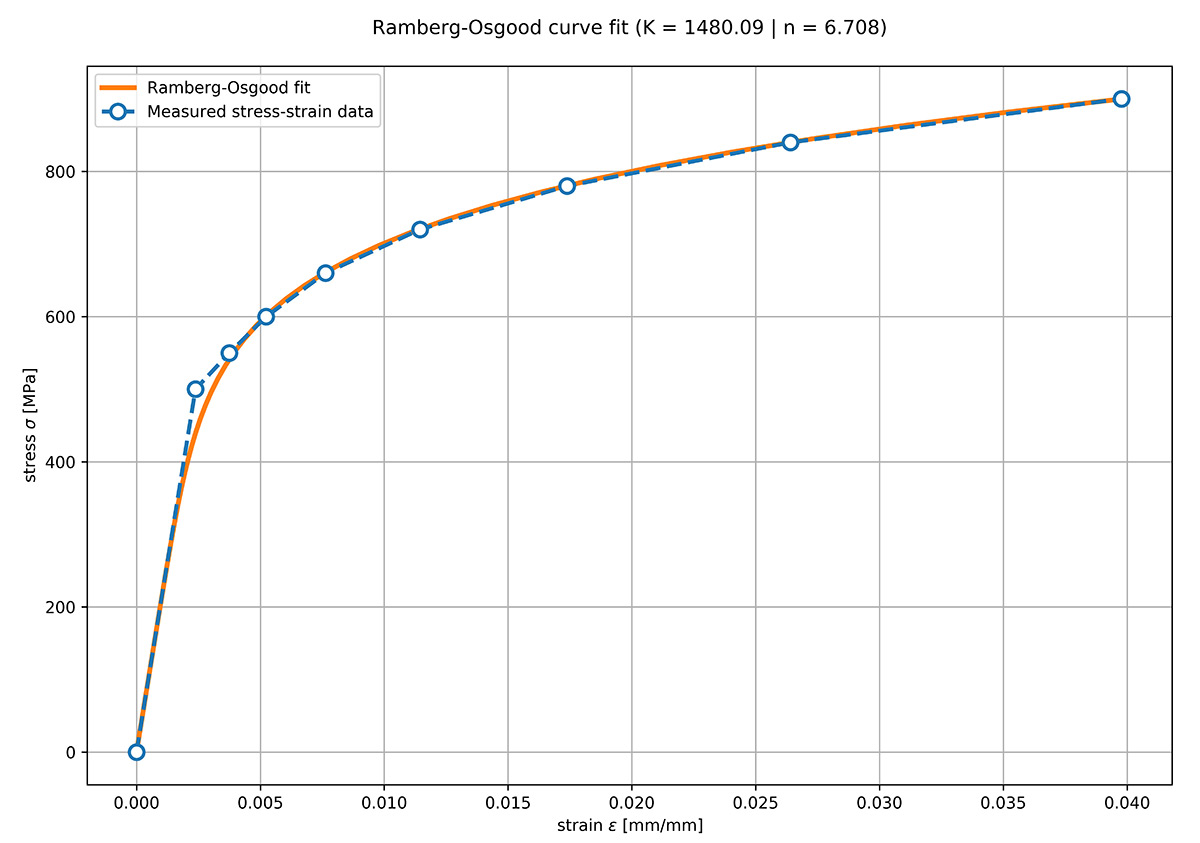
In Abbildung 1 werden die Spannungs-Dehnungs-Daten eines Kohlenstoffstahls mit einer Fließspannung σ_y = 500 MPa und einem Elastizitätsmodul E = 210 000 MPa dargestellt. Die Ramberg-Osgood-Kurve (K = 1480, n = 6,71) ist gegen die gemessenen Spannungs-Dehnungs-Daten aufgetragen. Der Fehler bei Spannungen zwischen null und etwa 350 MPa ist sehr gering, steigt aber bei Spannungen zwischen 400 und 550 MPa an.

Die Ramberg-Osgood-Kurve liefert die Materialeingabe für elastisch-plastische FEA-Berechnungen und ist gleichermaßen wichtig für die Ermüdungs- und Dauerhaftigkeitsanalyse, wo die zyklische Spannungs-Dehnungs-Kurve den lokalen Dehnungsbereich an Kerben und Spannungskonzentrationen bestimmt.

Wie passt man Spannungs-Dehnungs-Daten an die Ramberg-Osgood-Gleichung an?

Die Anpassung der Spannungs-Dehnungs-Daten an eine Ramberg-Osgood-Kurve kann mit Excel durchgeführt werden, aber auch z. B. mit Python. Der Python 3.x-Code ist nachfolgend bereitgestellt:

     
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt


# MATERIAL DATA
strain = np.array([0, 500/210000, 0.003749347, 0.005234888, 0.007631515, 
                   0.011446096, 0.017384888, 0.026405375, 0.039775799])
stress = np.array([0, 500, 550, 600, 660, 720, 780, 840, 900])
E = stress[1] / strain[1]  # CALCULATE YOUNG'S MODULUS

# FITTING RAMBERG-OSGOOD EQUATION
def test_func(x, K, n):
    return x / E + np.power(x / K, n)

p0 = [500, 5]  # Initial estimate for [K, n]
c, cov = curve_fit(test_func, stress, strain, p0)

# PRINT CURVE FIT PARAMETERS
print()
print('-' * 28)
print(' Ramberg-Osgood parameters')
print('-' * 28)
print(f' K = {c[0]} \n n = {c[1]}')
print('-' * 28)

# CREATE DATA ARRAY FOR THE FITTED CURVE
e = test_func(np.linspace(0, stress[-1]), c[0], c[1])  # STRAIN
s = np.linspace(0, stress[-1])  # STRESS

# PLOT DATA AND FITTED CURVE
plt.figure(1, figsize=(12, 8))
# PLOT FITTED CURVE:
plt.plot(e, s, lw=3, c='C1')
# PLOT MEASURED DATA:
plt.plot(strain, stress, '--o', lw=2.5, ms=9, mew=2, mfc='white', c='C0')
plt.grid()
plt.xlabel(r'Strain $\epsilon$ [mm/mm]')
plt.ylabel(r'Stress $\sigma$ [MPa]')
plt.title(f'Ramberg-Osgood curve fit (K = {np.round(c[0], 2)} '
          f'| n = {np.round(c[1], 3)})\n')
plt.legend(['Ramberg-Osgood fit', 'Stress-Strain measured data'])

plt.show()