De Ramberg-Osgood vergelijking beschrijft het niet-lineaire verband tussen de spanning en de vervorming van een materiaal rond de vloeigrens van het materiaal. De vergelijking wordt gebruikt om de spanning-rek curve te bepalen van een materiaal wanneer enkel de Ramberg-Osgood parameters van een materiaal gegeven zijn en niet de volledige spanning-rek data-set.
De Ramberg-Osgood verhouding
De wet van Hooke bepaalt dat onder de vloeigrens van een materiaal, de spanning recht evenredig is met de vervorming:
$${\sigma = {E} \; {\varepsilon}_{e}}$$
Ramberg en Osgood hebben een machtsfunctie opgesteld die de plastische vervorming van een materiaal beschrijft:
$${{\varepsilon}_{p} = \left(\frac{\sigma}{K} \right)^n}$$
De materiaalafhankelijke parameters $K$ en $n$ bepalen het verhardingsgedrag van het materiaal tijdens het vloeien.
De totale vervorming ${\varepsilon}_{t}$ is de som van de elastische vervorming ${\varepsilon}_{e}$ en de plastische vervorming ${\varepsilon}_{p}$, what resulteert in:
$${{\varepsilon}_{t} = {\varepsilon}_{e} + {\varepsilon}_{p} = \frac{\sigma}{E} + \left(\frac{\sigma}{K} \right)^n}$$
Met:
- $\varepsilon$ de vervorming
- $\sigma$ de spanning
- $K$ materiaal niet-lineaire modulus
- $n$ materiaal verhardingsexponent
Nauwkeurigheid van de vergelijking
De vergelijking levert geen perfecte voorstelling op van het werkelijke spanning-rek gedrag van een materiaal, omdat de Ramberg-Osgood vergelijking impliceert dat er bij elk spanningsniveau plastische vervorming optreedt, ook bij spanningen ver onder de vloeigrens. Het aandeel van de plastische vervorming in de totale vervorming is echter heel klein bij lage spanningsniveau's.
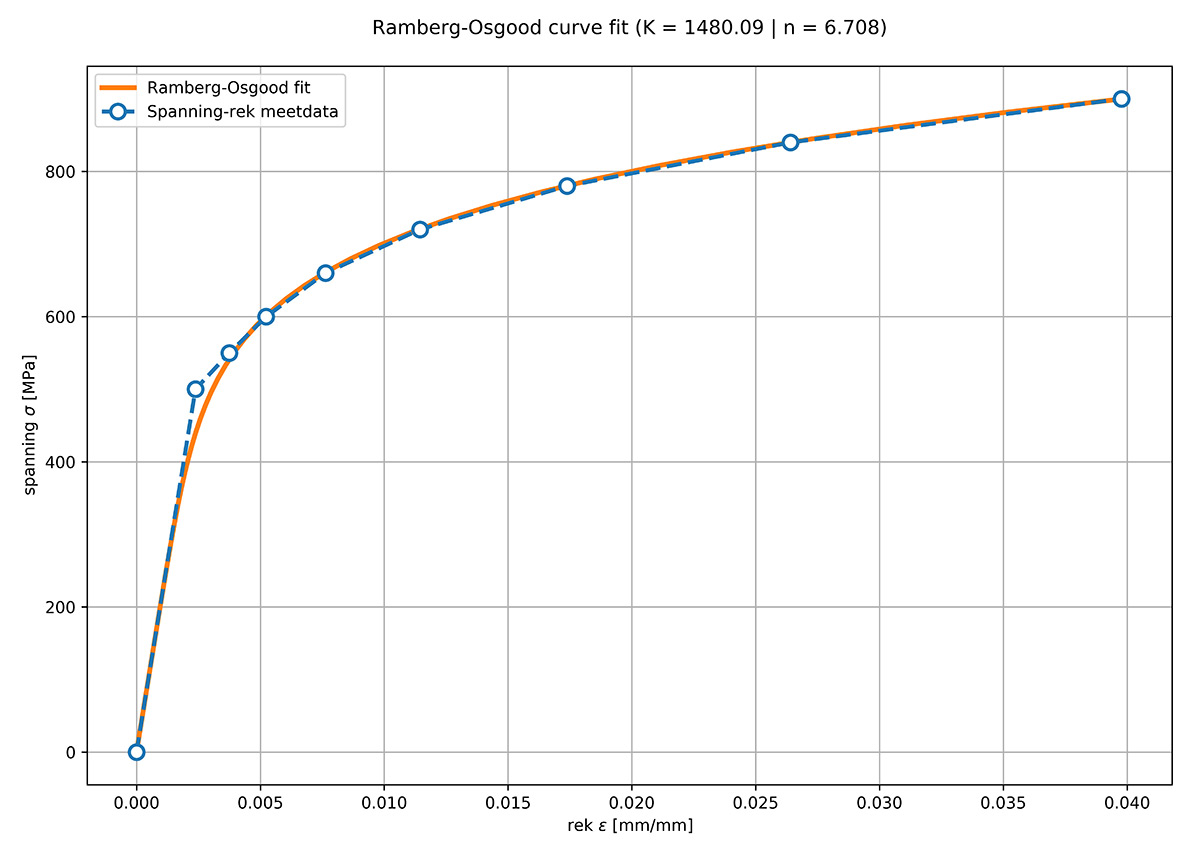
Verder vertonen sommige materialen een abrupte verandering van de stijfheid wanneer het materiaal begint te vloeien. In dat geval wijkt de Ramberg-Osgood aanzienlijk af van de werkelijke materiaalcurve bij spanningen rond het vloeipunt (zie Figuur 1 hieronder).
Een voorbeeld
In Figuur 1 is de spanning-rek data van een koolstofstaal met een vloeispanning σy = 500 MPa en een Elasticiteitsmodulus E = 210000 MPa weergegeven. De Ramberg-Osgood curve (K = 1480, n = 6.71) is uitgezet naast de spanning-rek meetdata. De fout tussen de meetdata en de curve-fit bij spanningen tussen nul en ongeveer 350 MPa is heel klein, maar wordt groter bij spanningen tussen 400 en 550 MPa.
Hoe worden de Ramberg-Osgood parameters van een materiaal bepaald?
Het fitten van de spanning-rek data in een Ramberg-Osgood curve kan met Excel gebeuren, maar ook met bv. Python.
Je kan via deze link de Python 3.x code van een Ramberg-Osgood curve fit programma downloaden.