The Ramberg-Osgood equation describes the nonlinear relationship between the stress and the strain of a material around the yield point of the material.
The Ramberg-Osgood relationship
Hooke's law states that below the yield point, the stress is linearly proportional to the strain:
$${\sigma = {E} \; {\varepsilon}_{e}}$$
Ramberg and Osgood defined a power-law to describe the plastic strain:
$${{\varepsilon}_{p} = \left(\frac{\sigma}{K} \right)^n}$$
The material dependent parameters $K$ and $n$ describe the hardening behaviour of the material.
The total strain ${\varepsilon}_{t}$ is the sum of the elastic strain ${\varepsilon}_{e}$ and the plastic strain ${\varepsilon}_{p}$, which results in:
$${{\varepsilon}_{t} = {\varepsilon}_{e} + {\varepsilon}_{p} = \frac{\sigma}{E} + \left(\frac{\sigma}{K} \right)^n}$$
With:
- ${\varepsilon}$ the strain
- ${\sigma}$ the stress
- $K$ material nonlinear modulus
- $n$ material strain-hardening exponent
Accuracy of the equation
The equation is not a perfect representation of the real material's stress-strain behaviour, because the Ramberg-Osgood equation implies that plastic strain is present at any stress level, also way below the yield point. However, the plastic strain part of the total strain is very small at low stress levels.
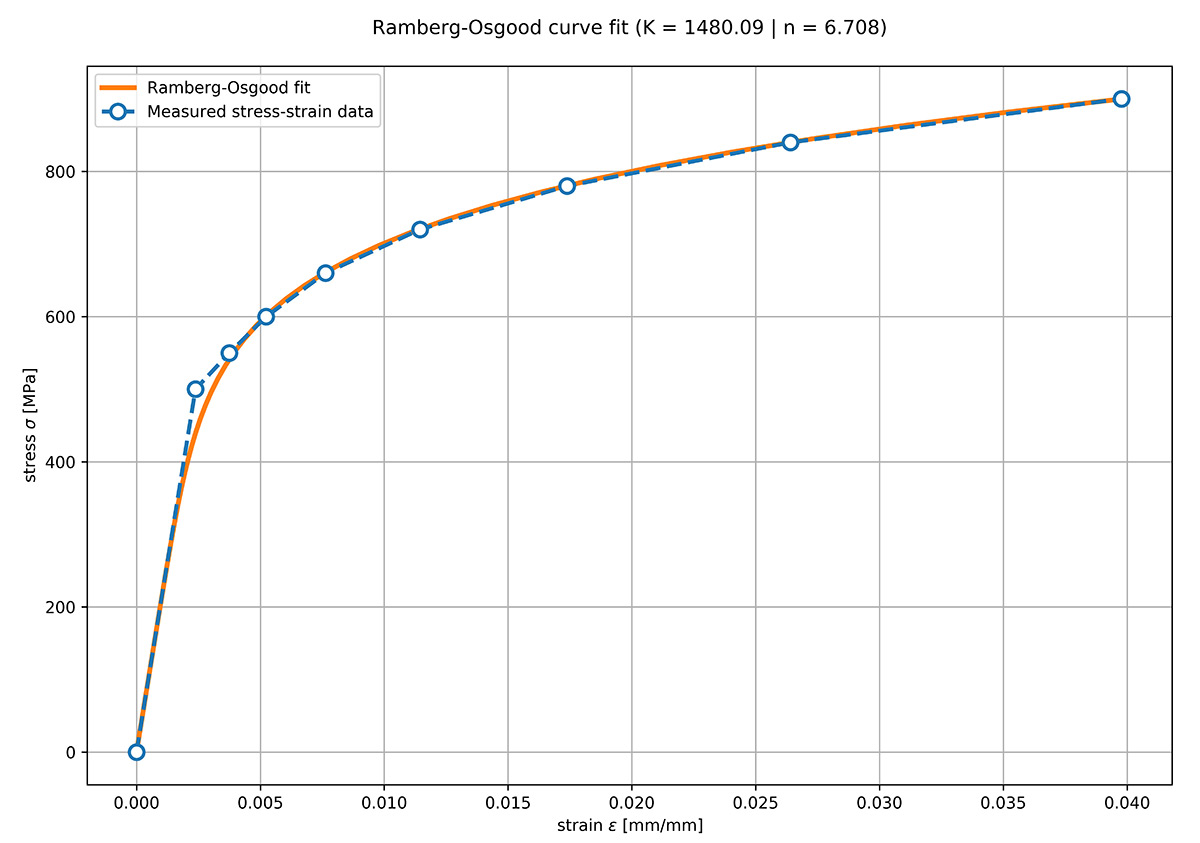
Some materials show an abrupt change of stiffness at yielding. In that case, the Ramberg-Osgood relationship doesn't hold well around the yield point (see Figure 1 below).
Example
In Figure 1, the stress-strain data of a carbon steel with a yield stress σy = 500 MPa and a Young's Modulus E = 210000 MPa is presented. The Ramberg-Osgood curve (K = 1480, n = 6.71) is plotted against the measured stress-strain data. The error at stresses between zero and around 350 MPa is very small, but increases at stresses between 400 and 550 MPa.
How to fit stress-strain data to the Ramberg-Osgood equation?
Fitting a curve to the stress-strain data can be done in Excel or with e.g. Python. You can download the source code of a Ramberg-Osgood curve fit algorithm written for Python 3.x.