What are the differences between high-cycle and low-cycle fatigue?

Material fatigue refers to the deterioration of a material caused by repeatedly applied loads, which can lead to structural failure or cracks over time. The distinction between high-cycle and low-cycle fatigue is crucial in understanding how materials behave under different stress conditions

What is High-Cycle Fatigue (HCF)?

High-cycle fatigue occurs when materials are subjected to stresses much lower than their yield strength, at a high number of cycles. Failure typically happens after millions of cycles due to microscopic cracks propagating over time. The emphasis in HCF is on the endurance of materials under relatively low stress levels but for a very high number of cycles. It is often associated with elastic deformation, meaning the material does not undergo (significant) permanent deformation before failure.

• Definition: HCF is identified when the fatigue life of a component spans a large number of cycles, typically 10⁵ cycles or more.
• Stress and Deformation: It involves lower stress levels, generally below the material's yield strength, which corresponds to an elastic behavior on a macro scale. The material does not undergo permanent deformation through the loading cycles.
• Cycle Count: The high number of cycles to failure reflects the lower stress levels involved, requiring more cycles for a crack to initiate and propagate to failure.
• Applications and Analysis: HCF is relevant in situations where a component is subjected to many cycles of relatively low stress, like parts in rotating machinery or structures subjected to vibrations. The stress–life (S–N) method is commonly used to predict the lifespan of components under HCF conditions by plotting stress range against the number of cycles to failure.
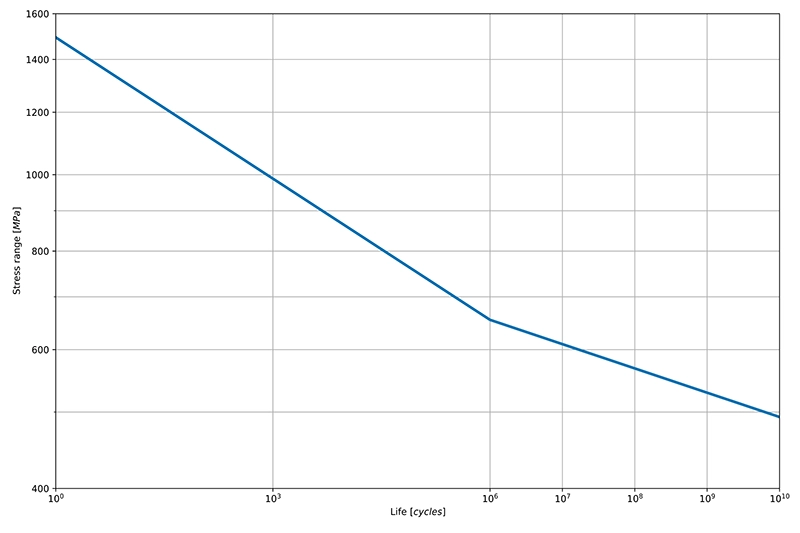
• Material curve: To predict high-cycle fatigue an S–N curve is used. The S–N curve, also known as the Wöhler curve, graphically represents the relationship between the stress range applied to a material and the number of cycles to failure. The vertical axis of the S–N curve represents the applied stress range. The horizontal axis represents the number of cycles to failure. The S–N curve is generally represented in a log–log plot (see figure 1 below).
• Material curve: To predict high-cycle fatigue an S–N curve is used. The S–N curve, also known as the Wöhler curve, graphically represents the relationship between the stress range applied to a material and the number of cycles to failure. The vertical axis of the S–N curve represents the applied stress range. The horizontal axis represents the number of cycles to failure. The S–N curve is generally represented in a log–log plot (see figure 1 below).

What is Low-Cycle Fatigue (LCF)?

LCF happens when materials are subjected to higher stresses, typically exceeding the yield strength, at a smaller number of cycles. This can lead to structural failure within thousands or even as low as hundreds of cycles. LCF is characterized by significant plastic deformation, where the material undergoes permanent changes in shape before breaking.

• Definition: LCF occurs when materials are subjected to loads at high amplitudes, leading to fatigue lives up to approximately 10⁴ cycles.
• Stress and Deformation: This condition is characterized by higher stress levels, often near or above the material's yield strength, resulting in macroplastic deformation during each cycle. This means the material undergoes permanent changes in shape that are visible at the macro scale.
• Cycle Count: Due to the higher stress and resultant plastic deformation, the number of cycles to failure is relatively low.
• Applications and Analysis: LCF is significant in scenarios where components are subjected to severe stress conditions that cause plastic deformation, such as engine parts under thermal stress. The strain–life (E–N or ε–N) method is typically employed for LCF analysis, taking into account both the elastic and plastic strain components to estimate the fatigue life.
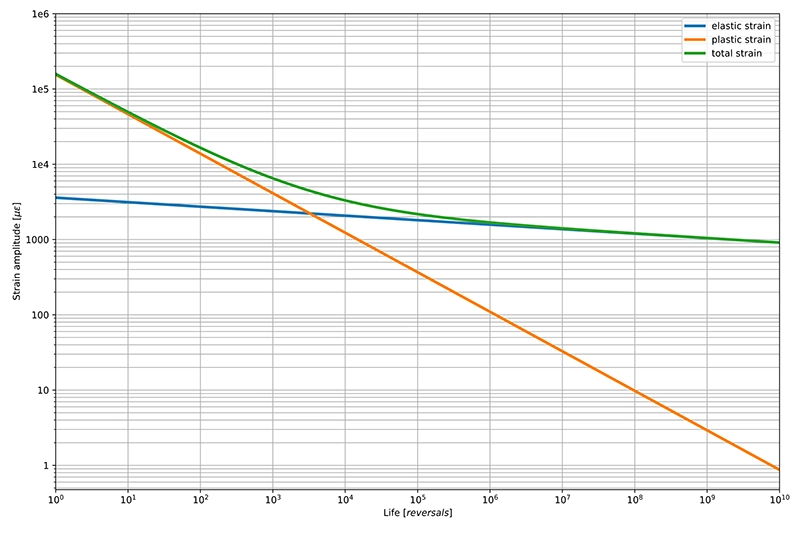
• Material curve: To predict low-cycle fatigue an E–N or ε–N curve is used. The ε–N curve, also known as the total strain–life curve, graphically represents the relationship between strain amplitude and the number of reversals to failure under cyclic loading conditions. The vertical axis of the ε–N curve represents the strain amplitude, which is half the range of strain in a complete loading and unloading cycle. Strain amplitude combines both elastic and plastic components of strain, reflecting the total deformation experienced by the material. The horizontal axis represents the number of reversals of applied strain that a material can endure before failure occurs. This can range from a relatively low number (hundreds to thousands) for materials under high strain conditions to much higher numbers under low strain conditions (see figure 2 below).

Key Differences between High-Cycle and Low-Cycle Fatigue

• The boundary between LCF and HCF is not defined by a precise number of cycles, but rather by the stress levels and the material's response — macroplastic deformation for LCF and elastic behavior for HCF.
• The primary distinction lies in the stress levels and the resultant deformation: LCF is associated with high stress and macroplastic deformation, whereas HCF involves lower stress and elastic deformation.
• Analysis methods differ between the two, with LCF using the strain–life method (E–N or ε–N method) for its emphasis on plastic deformation and HCF employing the stress–life method (S-N method) suited for elastic behavior analysis.

Understanding these nuances is essential for accurately predicting material failure, designing durable components, and ensuring the reliability of structures and machinery under varying conditions of stress and fatigue.