Materialermüdung
Glossar der Begriffe
- Wechselspannung
-
Wechselspannung bezieht sich auf die schwankende Spannung, die ein Material erfährt, wenn es zyklisch belastet wird. Sie ist definiert als die Differenz zwischen den maximalen und minimalen Spannungswerten innerhalb eines Belastungszyklus. Sie wird manchmal auch als Spannungsamplitude bezeichnet.
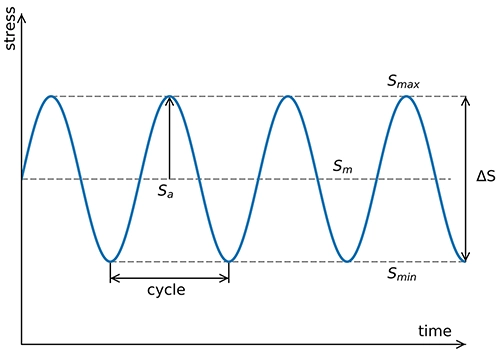
Abb. 1 Spannungsdefinitionen: Sa, Smin, Smax, Sm und ΔS
- Zyklische Spannungs-Dehnungs-Kurve
-
Die Verformung des Materials während eines Ermüdungstests wird in Form einer Hystereseschleife gemessen. Nach einem anfänglichen Übergangsverhalten stabilisiert sich das Material und dieselbe Hystereseschleife wird für jeden Belastungszyklus erhalten. Jede getestete Dehnungsreichweite hat eine entsprechende Spannungsreichweite, die gemessen wird. Die zyklische Spannungs-Dehnungs-Kurve ist ein Diagramm aller dieser Daten.
Die Kurve beschreibt das Verhalten des Materials, nachdem es plastisch verformt wurde. Dieses Verhalten unterscheidet sich in der Regel von dem anfänglichen Verhalten, das in einem herkömmlichen Zugversuch gemessen wird. Eine einfache Potenzfunktion wird an diese Kurve angepasst, um drei Materialeigenschaften zu erhalten: den zyklischen Festigkeitskoeffizienten K', den zyklischen Verfestigungsexponenten n' und den Elastizitätsmodul E.
- Dang Van Kriterium
-
Das Dang Van Kriterium ist ein Ermüdungsgrenzkriterium, das verwendet wird, um die Dauerfestigkeit unter komplexen, mehrachsigen Belastungssituationen vorherzusagen. Das Ergebnis der Analyse wird als Sicherheitsfaktor und nicht als Ermüdungslebensdauer ausgedrückt. Es verwendet spezifische Materialparameter, die aus Zug- und Torsionstests berechnet werden. Fertigungsprozesse können auch berücksichtigt werden, indem die äquivalente plastische Dehnung im unbelasteten Bauteil verwendet wird.
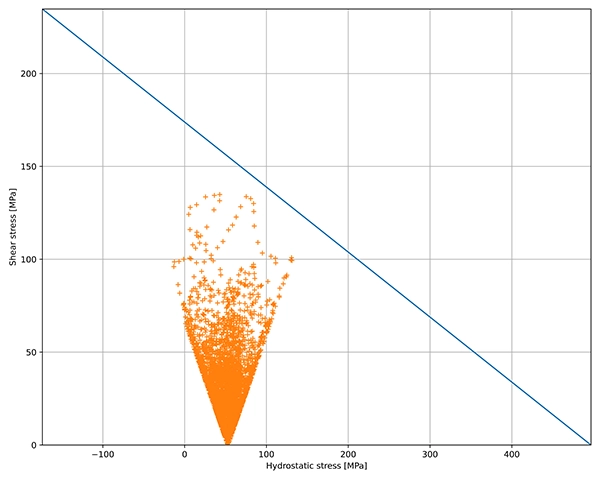
Abb. 2 Das Diagramm zeigt das Dang Van Streudiagramm (orange Punkte) am kritischen Element des Bauteils. Dieses Diagramm stellt dar, wie der Belastungspfad in Bezug auf die mikroskopische Scherspannung und den hydrostatischen Druck in Bezug auf das Ermüdungskriterium (blaue Linie) liegt. Grundsätzlich bedeutet dies, dass ein Versagen auftritt, wenn das Streudiagramm die blaue Diagonallinie überschreitet.
- Schadensverzeihendes Design
-
Dieser Ansatz im Design gegen Ermüdung erkennt an, dass während der Lebensdauer des Bauteils oder der Struktur Schäden (wie Risse) auftreten werden. Das Design muss das Vorhandensein von Schäden ohne katastrophales Versagen tolerieren und einen sicheren Betrieb bis zur Entdeckung und Reparatur der Schäden ermöglichen. Dies erfordert ein Verständnis des Schadenswachstums im Laufe der Zeit, den Einsatz zerstörungsfreier Prüfmethoden (NDT) zur Überwachung von Schäden und die Festlegung von Inspektionsintervallen basierend darauf, wie schnell sich Schäden auf eine kritische Größe ausbreiten können. Es ist ein proaktiver Ansatz, der darauf abzielt, Sicherheit und Integrität auch im Falle unerwarteter Schäden zu gewährleisten.
Siehe auch unendliche Lebensdauer, sichere Lebensdauer und ausfallsicheres Design.
- Dauerfestigkeit
-
In Labortests getestete Stahlproben zeigen eine sichere Spannung, unterhalb derer kein Versagen auftritt. Diese sichere Spannung wird als Dauerfestigkeit oder Ermüdungsgrenze bezeichnet. Dieses Verhalten wird nur bei Stahl beobachtet. Bei Aluminiumlegierungen wird normalerweise eine Ermüdungsfestigkeit bei 107 Zyklen anstelle der Ermüdungsgrenze verwendet. Dies ist eine Spannung, die bei 107 Zyklen zu Versagen führt.
- Ausfallsicheres Design
-
Dieser Designansatz gegen Ermüdung basiert auf der Annahme, dass ein gewisses Maß an Schaden oder Versagen unvermeidlich ist. Der Fokus liegt darauf, sicherzustellen, dass ein solches Versagen nicht zu katastrophalen Folgen führt. Dies wird durch den Einbau von Redundanzen erreicht, durch die Gestaltung von Bauteilen, die auf nicht-katastrophale Weise versagen, oder durch die Bereitstellung alternativer Lastpfade, sodass, wenn ein Bauteil versagt, die gesamte Struktur die Lasten weiterhin sicher tragen kann. Diese Philosophie ist in Systemen verbreitet, bei denen das Versagen eines einzelnen Bauteils zu erheblichen Gefahren führen könnte, wie beispielsweise in Flugzeugstrukturen.
Siehe auch unendliche Lebensdauer, ausfallsicheres Design und schadensverzeihendes Design.
- Ermüdungsgrenze
-
Siehe Dauerfestigkeit
- Kerbfaktor
-
Experimente haben gezeigt, dass die Wirkung kleiner Kerben geringer ist als die, die aus dem traditionellen Spannungskonzentrationsfaktor Kt abgeleitet wird. Der Kerbfaktor Kf kann als effektive Spannungskonzentration bei Ermüdung betrachtet werden. Er hängt von der Größe der Spannungskonzentration und dem Material ab. Kleine Spannungskonzentrationen sind in hochfesten Materialien wirksamer. Dieser Effekt wird mit einem Kerbempfindlichkeitsfaktor q behandelt:
$${\displaystyle {K _{f}} = 1 + ({{K _{t}} - 1})\cdot{q}}$$
Der Kerbempfindlichkeitsfaktor q ist eine empirisch bestimmte Konstante, die vom Kerbradius und der Materialfestigkeit abhängt.
- Ermüdungsfestigkeit
-
Die Spannung, die erforderlich ist, um Versagen in einer bestimmten Anzahl von Zyklen zu erzeugen. Bei Stahl sind dies normalerweise 106 Zyklen und bei Schweißnähten und Aluminiumlegierungen 107 Zyklen. Sie hängt direkt von der Festigkeit des Materials ab.
Eine nützliche Annäherung für die Ermüdungsfestigkeit ist die Hälfte der Zugfestigkeit.
- Goodman-Diagramm
-
Zugmittelspannungen verringern die Ermüdungslebensdauer im Vergleich zu vollständig umgekehrter Belastung. Das Goodman-Diagramm, das ursprünglich 1890 vorgeschlagen wurde, ist eine grafische Darstellung dieses Effekts.
Die Wechselspannung wird auf einer Achse und die Mittelspannung auf der anderen Achse aufgetragen. Die zulässige Wechselspannung ohne Mittelspannung ist die Ermüdungsgrenze. Die maximale Mittelspannung bei null Wechselspannung ist die Zugfestigkeit. Eine gerade Linie wird dann zwischen den beiden Punkten gezogen. Jede Kombination von Mittel- und Wechselspannung auf dieser Linie wird die gleiche Ermüdungslebensdauer haben. Mathematisch kann dies ausgedrückt werden als:
$$\frac{S_a}{S_f} + \frac {S_m}{S_u} = 1$$
Sa ist die Wechselspannung, Sf die vollständig umgekehrte Spannung mit null Mittelspannung, Sm die Mittelspannung und Su die Zugfestigkeit.
- Hochzyklische Ermüdung
-
Die hochzyklische Ermüdung ist eine Art von Ermüdungsversagen, das in einem Material auftritt, wenn es einer großen Anzahl von Lastzyklen ausgesetzt ist, typischerweise mehr als 105 oder sogar Millionen von Zyklen. Hochzyklische Ermüdung ist durch relativ geringe Spannungsamplituden gekennzeichnet und beinhaltet oft geringere Verformungen im Vergleich zur niedrigzyklischen Ermüdung.
- Hystereseschleife
-
Die Spannungs-Dehnungs-Antwort eines Materials, das zyklisch belastet wird, erfolgt in Form einer Hystereseschleife.
Die Hystereseschleife ist oft durch ihre Spannungsreichweite Δσ und Dehnungsreichweite Δε gekennzeichnet. Die Dehnungsreichweite wird oft in den elastischen Teil und den plastischen Teil aufgeteilt.
- Unendliche Lebensdauer
-
Dieser Designansatz gegen Ermüdung zielt darauf ab, dass das Bauteil oder die Struktur einer unendlichen Anzahl von Lastzyklen standhält, ohne zu versagen, vorausgesetzt, die Lasten überschreiten nicht eine bestimmte Schwelle, die als Dauerfestigkeit bekannt ist. Wenn die angewendeten Spannungen unter diesem Niveau gehalten werden, sollte das Bauteil theoretisch nie aufgrund von Ermüdung versagen. Dieser Ansatz wird häufig bei kritischen Bauteilen verwendet, bei denen ein Versagen keine Option ist, kann jedoch zu übermäßigem Bauteilgewicht und erhöhten Kosten führen.
Siehe auch sichere Lebensdauer, ausfallsicheres Design und schadensverzeihendes Design.
- Belastungsfaktor
-
Historisch gesehen wurden Ermüdungsgrenzen aus einfachen Biegeversuchen bestimmt, bei denen es einen Spannungsgradienten im Teststück gibt. Ein unter Zug beanspruchtes Teststück hat eine niedrigere Ermüdungsgrenze als eines, das unter Biegung belastet wird. Ein empirischer Korrekturfaktor, genannt Belastungsfaktor, wird verwendet, um diesen Effekt zu berücksichtigen.
- Niedrigzyklische Ermüdung
-
Die niedrigzyklische Ermüdung ist eine Art von Ermüdungsversagen, das in Materialien auftritt, wenn sie hohen Spannungsamplituden ausgesetzt sind und sich über eine relativ geringe Anzahl von Lastzyklen erheblich plastisch verformen, typischerweise weniger als 104–105 Zyklen. Siehe auch hochzyklische Ermüdung
- Mittelspannung
-
Die Mittelspannung Sm ist der Durchschnittswert der Spannungen.
Siehe Abb. 1 Spannungsdefinitionen
- Neubers Regel
-
Neubers Regel wird verwendet, um eine elastisch berechnete Spannung oder Dehnung in die tatsächliche Spannung oder Dehnung umzuwandeln, wenn eine plastische Verformung auftritt. Beispielsweise können wir eine Spannung mit elastischen Annahmen an einer Kerbe als KtS berechnen, und diese Spannung überschreitet die Festigkeit des Materials. Die tatsächliche Spannung wird irgendwo auf der Spannungs-Dehnung-Kurve des Materials bei einem Punkt σ liegen.
Neubers Regel besagt, dass das Produkt aus der elastischen Spannungs- und Dehnungslösung gleich dem Produkt der tatsächlichen elastoplastischen Lösung ist. Mathematisch wird dies ausgedrückt als:
$${\displaystyle {K _{t}}{S}\cdot{K _{t}}{e}={\sigma}\cdot{\varepsilon}}$$
- Nennspannung
-
Die Nennspannung ist die Spannung, die fern von lokalen Spannungskonzentrationen liegt.
- Nennspannung
-
Die Nennspannung ist die Spannung, die fern von lokalen Spannungskonzentrationen liegt.
- Redundanz
-
Im Kontext des Bauingenieurwesens bezieht sich Redundanz auf das Konstruktionsprinzip, bei dem eine Struktur mit zusätzlichen Elementen oder alternativen Lastpfaden gebaut wird, die für die Tragfähigkeit der Struktur unter normalen Bedingungen nicht unbedingt erforderlich sind. Dieser Konstruktionsansatz erhöht die Fähigkeit der Struktur, ihre beabsichtigte Funktion auch bei Versagen eines oder mehrerer struktureller Komponenten weiterhin zu erfüllen. Redundanz in Strukturen ist ein wesentlicher Aspekt zur Gewährleistung von Sicherheit und Zuverlässigkeit, insbesondere in Umgebungen, in denen das Versagen eines einzelnen Elements zu katastrophalen Folgen führen könnte.
Siehe auch ausfallsicheres Design.
- Sichere Lebensdauer
-
Der sichere Lebensdaueransatz bezieht sich auf eine Konstruktionsmethode, bei der Komponenten so ausgelegt sind, dass sie eine begrenzte Betriebslebensdauer unter bestimmten Lasten oder Spannungen haben. Dieser Ansatz wird häufig in verschiedenen Branchen wie der Automobilindustrie, bei Druckbehältern und in der Strahltriebwerkskonstruktion verwendet. Die sichere Lebensdauerberechnung umfasst eine Sicherheitsmarge für die Streuung der Ermüdungsergebnisse und andere unbekannte Faktoren, und die Berechnungen können auf Spannungslebensdauer, Dehnungslebensdauer oder Risswachstumsbeziehungen basieren. Feld- und Simulationstests spielen eine Schlüsselrolle bei der Bestimmung der sicheren Lebensdauer für Produkte wie Strahltriebwerke, Kanonenrohre und Lager.
Siehe auch unendliche Lebensdauer, ausfallsicheres Design und schadensverzeihendes Design.
- Sicherheitsfaktor
-
Der Sicherheitsfaktor gibt an, um wie viel Sie die maximale Festigkeit der Materialien unterschätzen möchten, um ein sicheres Design zu gewährleisten. Ein einzelner Sicherheitsfaktor wird sowohl auf die Spannungsamplitude als auch auf die Mittelspannung angewendet.
Dies kann grafisch im Goodman-Diagramm dargestellt werden.
- Größenfaktor
-
Experimentell haben größere Teile niedrigere Ermüdungsgrenzen als kleinere Teile. Da die Materialdaten von kleinen Proben erhalten werden, wird für größere Durchmesser ein Korrekturfaktor, genannt Größenfaktor, verwendet. Für nicht kreisförmige Querschnitte wird ein effektiver Durchmesser berechnet. Der effektive Durchmesser wird durch Gleichsetzung des Volumens des Materials, das 95% der maximalen Spannung ausgesetzt ist, mit einem Rundstab im Biegeprozess berechnet, der das gleiche hoch belastete Volumen hat.
- Dehnungsamplitude
-
Die Dehnungsamplitude ist die Hälfte der Dehnungsreichweite.
- Dehnungs-Lebensdauer-Kurve
-
Die Dehnungs-Lebensdauer-Kurve, auch bekannt als εε-N-Kurve, ist ein grundlegendes Konzept im Bereich der Materialermüdungsanalyse, das eine Methode zur Vorhersage der Ermüdungslebensdauer von Materialien unter zyklischer Belastung basierend auf ihrer Dehnungsantwort bietet. Der Dehnungs-Lebensdauer-Ansatz kombiniert sowohl elastische als auch plastische Dehnungskomponenten, um die Haltbarkeit von Materialien über eine breite Palette von Lastzyklen zu bewerten. Diese Methode ist besonders nützlich für Szenarien mit niedrigzyklischer Ermüdung, bei denen signifikante plastische Verformungen auftreten.
Die Dehnungs-Lebensdauer-Kurve wird durch zwei Hauptbeziehungen dargestellt: die Basquin-Gleichung für die elastische Dehnungskomponente und die Manson-Coffin-Beziehung für die plastische Dehnungskomponente. Die Basquin-Gleichung, die 1910 vorgeschlagen wurde, beschreibt den Zusammenhang zwischen der elastischen Dehnungsamplitude und der Ermüdungslebensdauer, während die Manson-Coffin-Beziehung, die in den frühen 1960er Jahren entwickelt wurde, eine Korrelation zwischen der plastischen Dehnungsamplitude und der Ermüdungslebensdauer herstellt. Diese Gleichungen zusammen beschreiben, wie Materialien auf zyklische Spannungen und Dehnungen reagieren, und ermöglichen die Schätzung der Ermüdungslebensdauer anhand einer Kombination aus elastischen und plastischen Dehnungskomponenten.
- Dehnungsreichweite
-
Die Dehnungsreichweite Δε ist die maximale Dehnung minus der minimalen Dehnung in einem Zyklus.
- Spannungsamplitude
-
Die Spannungsamplitude Sa ist der Betrag, um den die Spannung von der Mittelspannung abweicht. Sie wird manchmal auch als Wechselspannung bezeichnet.
Siehe Abb. 1 Spannungsdefinitionen
- Spannungskonzentrationsfaktor
-
Spannungskonzentrationen entstehen durch jede abrupte Änderung der Geometrie eines unter Last stehenden Bauteils. Infolgedessen ist die Spannungsverteilung im Querschnitt nicht gleichmäßig.
Zum Beispiel ist es oft notwendig, ein Loch in eine Platte zu bohren. Wenn eine Last P angewendet wird, stört das Vorhandensein des Lochs die gleichmäßige Nennspannung in der Platte.
Das Profil der Spannung im Querschnitt durch die Mitte des Lochs hat die Form, die in der folgenden Abbildung (blaue Farbe) gezeigt wird. Beachten Sie, dass die maximale Spannung σmax Kt · σnom beträgt und am Rand des Lochs auftritt. Der Faktor Kt ist als Spannungskonzentrationsfaktor bekannt.
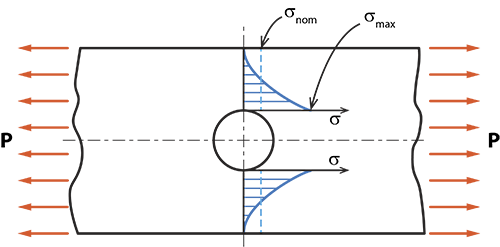
Abb. 3 Spannungskonzentration um ein Loch in einer Platte
- Spannungs-Lebensdauer-Kurve
-
Die Spannungs-Lebensdauer (S-N) Kurve, auch bekannt als Wöhler-Kurve, ist eine grafische Darstellung der Beziehung zwischen dem angewendeten Spannungsniveau und der Ermüdungslebensdauer eines Materials. Sie ist ein grundlegendes Werkzeug in der Ermüdungsanalyse und -konstruktion. Die S-N-Kurve zeigt das Spannungsniveau (S), das erforderlich ist, um in einer bestimmten Anzahl von Zyklen (Nf) zum Versagen zu führen.
Die S-N-Kurve zeigt typischerweise eine kontinuierlich abfallende Kurve mit geringerer Variabilität der Lebensdauer bei kürzeren Lebensdauern und größerer Variabilität bei längeren Lebensdauern. Diese Variabilität kann von weniger als einem Faktor 2 bis zu mehr als einer oder zwei Größenordnungen reichen.
Bei einigen Materialien kann zwischen 106 und 107 Zyklen unter nicht korrosiven Bedingungen eine Diskontinuität oder "Knie" in der S-N-Kurve beobachtet werden. Bei den meisten Materialien tritt jedoch dieses Knie nicht auf, und in korrosiven Umgebungen haben alle S-N-Daten ausnahmslos eine kontinuierlich abfallende Kurve.
- Spannungsbereich
-
Der Spannungsbereich ΔS ist die Spitzen-zu-Spitzen-Spannung.
Siehe Abb. 1 Spannungsdefinitionen
- Oberflächenfinishfaktor
-
Die Ermüdungsgrenzen werden aus kleinen polierten Laborproben bestimmt. Ein Oberflächenfinishkorrekturfaktor wird an der Ermüdungsgrenze des Materials vorgenommen, um eine Schätzung der Ermüdungsgrenze des Bauteils im tatsächlichen Einsatzzustand zu erhalten.
Weitere Informationen über den Einfluss der Oberflächenqualität auf die Ermüdungslebensdauer finden Sie unter Oberflächenrauheitsfaktor KR.
- Zugfestigkeit
-
Die Zugfestigkeit Su wird auch als maximale Festigkeit bezeichnet. Sie ist die maximale Spannung, die in einem Spannungs-Dehnungs-Diagramm erreicht wird.
Unsere Kurse
Wenn Sie mehr darüber erfahren möchten, wie Sie die Finite-Elemente-Methode effizienter in Ihren Designs einsetzen können, dann könnte unser Kurs Praktische Einführung in die Finite-Elemente-Methode oder unser Kurs Einführung in die Ermüdungsanalyse mit FEA für Sie interessant sein.